5、(2011•苏州)有一组数椐：3，4，5，6，6，则下列四个结论中正确的是(　)

　　 A、这组数据的平均数、众数、中位数分别是4.8，6，6　　　　 B、这組数据的平均数、众数、中位数分别是5，5，5

　　 C、这组数据的平均数、众数、中位数分别是4.8，6，5　　　　 D、这组数据的平均数、众数、中位数分别是5，6，6

考点：众数；算术平均数；中位数。

专题：计算题。

分析：要求平均数只要求出数据之和再除以总个数即可；对于众数可由数据中出现次数最多的数写出；对于中位数，因为题中是按从小到大的顺序排列的，所以只要找出最中间的一个数(或最中间的两个数)即可，本题是最中间的一个数．

解答：解：一组数椐：3，4，5，6，6的平均数=(3+4+5+6+6)÷5=24÷5=4.8．

6出现的次数最多，故众数是6．

按从小到大的顺序排列，最中间的一个数是5，故中位数为：5．

故选C．

点评：本题考查平均数、中位数和众数的概念．一组数据的总和除以这组数据个数所得到的商叫这组数据的平均数；在一组数据中出现次数最多的数叫做这组数据的众数；将一组数据从小到大依次排列，把中间数据(或中间两数据的平均数)叫做中位数．

4、(2011•苏州)若m•2³=2⁶，则m等于(　)

　　 A、2　　　　 B、4

　　 C、6　　　　 D、8

考点：同底数幂的除法。

专题：计算题。

分析：根据乘除法的关系，把等式变形，根据同底数幂的除法，底数不变指数相减．

解答：解；m=2⁶÷2³=2^6﹣3=2³=8，

故选：D，

点评：此题主要考查了同底数幂的除法，题目比较基础，一定要记准法则才能做题．

3、(2010•清远)地球上的海洋面积约为361000000千米²，将361000000这个数用科学记数法表示为(　)

　　 A、3.61×10⁸　　 B、3.61×10⁷

　　 C、361×10⁷　　 D、0.361×10⁹

考点：科学记数法-表示较大的数。

专题：应用题。

分析：科学记数法的表示形式为a×10ⁿ的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值大于1时，n是正数；当原数的绝对值小于1时，n是负数．

解答：解：将361 000 000用科学记数法表示为3.61×10⁸．

故选A．

点评：此题考查科学记数法的表示方法．科学记数法的表示形式为a×10ⁿ的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．

2、(2011•苏州)△ABC的内角和为(　)

　　 A、180°　　　　 B、360°

　　 C、540°　　　　 D、720°

考点：三角形内角和定理。

分析：根据三角形的内角和定理直接得出答案．

解答：解：三角形的内角和定理直接得出：△ABC的内角和为180°．

故选A．

点评：此题主要考查了三角形的内角和定理，此题比较简单注意正确记忆三角形内角和定理．

1、(2011•苏州)2×(﹣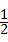)的结果是(　)

　　 A、﹣4　　　 B、﹣1

　　 C、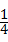　　　　 D、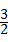

考点：有理数的乘法。

专题：计算题。

分析：根据有理数乘法法则：异号得负，并把绝对值相乘来计算．

解答：解：2×(﹣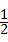)=﹣(2×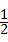)=﹣1．

故选B．

点评：考查了有理数的乘法法则：两数相乘，同号得正，异号得负，并把绝对值相乘．

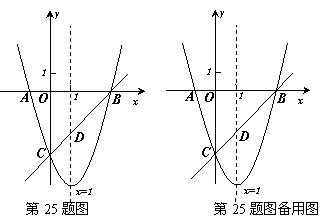
25．如图，已知抛物线y=x²+bx+c与x轴交于A、B两点(A点在B点左侧)，与y轴交于点C(0，－3)，对称轴是直线x=1，直线BC与抛物线的对称轴交于点D．

⑴求抛物线的函数表达式；

⑵求直线BC的函数表达式；

⑶点E为y轴上一动点，CE的垂直平分线交CE于点F，交抛物线于P、Q两点，且点P在第三象限．

①当线段PQ=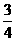AB时，求tan∠CED的值；

②当以点C、D、E为顶点的三角形是直角三角形时，请直接写出点P的坐标．

温馨提示：考生可以根据第⑶问的题意，在图中补出图形，以便作答．

24．已知，△ABC为等边三角形，点D为直线BC上一动点(点D不与B、C重合)．以AD为边作菱形ADEF，使∠DAF=60°，连接CF．

⑴如图1，当点D在边BC上时，

求证：∠ADB=∠AFC；②请直接判断结论∠AFC=∠ACB+∠DAC是否成立；

⑵如图2，当点D在边BC的延长线上时，其他条件不变，结论∠AFC=∠ACB+∠DAC是否成立？请写出∠AFC、∠ACB、∠DAC之间存在的数量关系，并写出证明过程；

⑶如图3，当点D在边CB的延长线上时，且点A、F分别在直线BC的异侧，其他条件不变，请补全图形，并直接写出∠AFC、∠ACB、∠DAC之间存在的等量关系．

23．一玩具厂去年生产某种玩具，成本为10元/件，出厂价为12元/件，年销售量为2万件．今年计划通过适当增加成本来提高产品档次，以拓展市场．若今年这种玩具每件的成本比去年成本增加0.7x倍，今年这种玩具每件的出厂价比去年出厂价相应提高0.5x倍，则预计今年年销售量将比去年年销售量增加x倍(本题中0＜x≤11)．

⑴用含x的代数式表示，今年生产的这种玩具每件的成本为________元，今年生产的这种玩具每件的出厂价为_________元．

⑵求今年这种玩具的每件利润y元与x之间的函数关系式．

⑶设今年这种玩具的年销售利润为w万元，求当x为何值时，今年的年销售利润最大？最大年销售利润是多少万元？

注：年销售利润=(每件玩具的出厂价－每件玩具的成本)×年销售量．

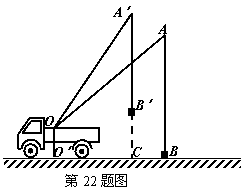22．小刘同学在课外活动中观察吊车的工作过程，绘制了如图所示的平面图形．已知吊车吊臂的支点O距离地面的高OO′=2米．当吊臂顶端由A点抬升至A′点(吊臂长度不变)时，地面B处的重物(大小忽略不计)被吊至B′处，紧绷着的吊缆A′B′=AB．AB垂直地面O′B于点B，A′B′垂直地面O′B于点C，吊臂长度OA′=OA=10米，且cosA=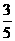，sinA′=．

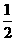⑴求此重物在水平方向移动的距离BC；

⑵求此重物在竖直方向移动的距离B′C．(结果保留根号)

20．某班数学兴趣小组收集了本市4月份30天的日最高气温的数据，经过统计分析获得了两条信息和一个统计表

信息1　 4月份日最高气温的中位数是15.5℃；

信息2　 日最高气温是17℃的天数比日最高气温是18℃的天数多4天．

4月份日最高气温统计表

请根据上述信息回答下列问题：

⑴4月份最高气温是13℃的有________天，16℃的有_______天，17℃的有__________天.

⑵4月份最高气温的众数是________℃，极差是_________℃。

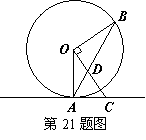
21．如图，点A、B在⊙O上，直线AC是⊙O的切线，OD⊥OB，连接AB交OC于点D．

⑴求证：AC=CD

⑵若AC=2，AO=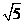，求OD的长度．