
题目列表(包括答案和解析)
28、(2011•苏州)如图①,小慧同学把一个正三角形纸片(即△OAB)放在直线l1上.OA边与直线l1重合,然后将三角形纸片绕着顶点A按顺吋针方向旋转120°,此时点O运动到了点O1处,点B运动到了点B1处;小慧又将三角形纸片AO1B1,绕点B1按顺吋针方向旋转 120°,此时点A运动到了点A1处,点O1运动到了点O2处(即顶点O经过上述两次旋转到达O2处).
小慧还发现:三角形纸片在上述两次旋转的过程中.顶点O运动所形成的图形是两段圆弧,即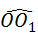 和
和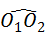 ,顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧与直线l1围成的图形面积等于扇形A001的面积、△AO1B1的面积和扇形B1O1O2的面积之和.
,顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧与直线l1围成的图形面积等于扇形A001的面积、△AO1B1的面积和扇形B1O1O2的面积之和.
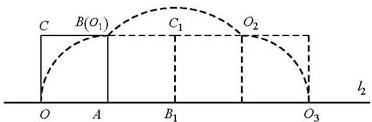
小慧进行类比研究:如图②,她把边长为1的正方形纸片0ABC放在直线l2上,0A边与直线l2重合,然后将正方形纸片绕着顶点A按顺时针方向旋转90°,此时点O运动到了点O1处(即点B处),点C运动到了点C1处,点B运动到了点B2处,小慧又将正方形纸片 AO1C1B1绕顶点B1按顺时针方向旋转90°,….按上述方法经过若干次旋转后,她提出了如下问题:
问题①:若正方形纸片0ABC按上述方法经过3次旋转,求顶点0经过的路程,并求顶点O在此运动过程中所形成的图形与直线l2围成图形的面积;若正方形纸片OABC按上述方法经过5次旋转.求顶点O经过的路程;
问题②:正方形纸片OABC按上述方法经过多少次旋转,顶点0经过的路程是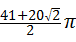 ?
?

考点:旋转的性质;等边三角形的性质;正方形的性质;弧长的计算;扇形面积的计算。
专题:几何图形问题。
分析:①根据正方形旋转3次和5次的路径,利用弧长计算公式以及扇形面积公式求出即可,
②再利用正方形纸片OABC经过4次旋转得出旋转路径,进而得出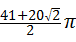 =20(1+
=20(1+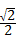 )π+
)π+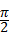 ,即可得出旋转次数.
,即可得出旋转次数.
解答:解:①如图所示,正方形纸片OABC经过3次旋转,顶点O运动所形成的图形是三段圆弧,
∴顶点O在此过程中经过的路程为: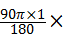 2+
2+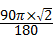 =(1+
=(1+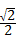 )π,
)π,
顶点O在此过程中经过的图形与直线l2围成的图形面积为:
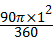 ×2+
×2+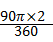 +2×
+2×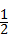 ×1=1+π.
×1=1+π.
正方形纸片OABC经过5次旋转,顶点O在此过程中经过的路程为:
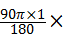 3+
3+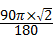 =(
=(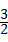 +
+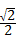 )π,
)π,
②正方形纸片OABC经过4次旋转,顶点O在此过程中经过的路程为:
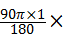 2+
2+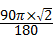 =(1+
=(1+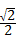 )π,
)π,
∴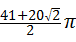 =20(1+
=20(1+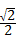 )π+
)π+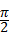 ,
,
∴正方形纸片OABC经过了81次旋转.
点评:此题主要考查了图形的旋转以及扇形面积公式和弧长计算公式,分别得出旋转3,4,5次旋转的路径是解决问题的关键.
27、(2011•苏州)已知四边形ABCD是边长为4的正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PB、PC、PD.

(1)如图①,当PA的长度等于 2 时,∠PAD=60°;当PA的长度等于 2
时,∠PAD=60°;当PA的长度等于 2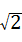 或
或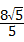 时,△PAD是等腰三角形;
时,△PAD是等腰三角形;
(2)如图②,以AB边所在直线为x轴、AD边所在直线为y轴,建立如图所示的直角坐标系(点A即为原点O),把△PAD、△PAB、△PBC的面积分别记为S1、S2、S3.设P点坐标为(a,b),试求2S1S3﹣S22的最大值,并求出此时a、b的值.
考点:相似三角形的判定与性质;二次函数的最值;正方形的性质;圆周角定理;解直角三角形。
专题:几何综合题;数形结合;方程思想。
分析:(1)由AB是直径,可得∠APB=90°,然后利用三角函数即可求得PA的长;当PA=PB时,△PAB是等腰三角形,然后由等腰三角形的性质与射影定理即可求得答案.
(2)过点P分别作PE⊥AB,PF⊥AD,垂足分别为E,F延长FP交BC于点G,则PG⊥BC,P点坐标为(a,b),PE=b,PF=a,PG=4﹣a,利用矩形的面积关系与二次函数的知识即可求得答案.
解答:解:(1)若∠PAD=60°,需∠PAB=30°,
∵AB是直径,
∴∠APB=90°,
∴PB=2,
则PA=2 ,
,
∴当PA的长度等于2 时,∠PAD=60°;
时,∠PAD=60°;
 若△PAD是等腰三角形,则只能是PA=PD,
若△PAD是等腰三角形,则只能是PA=PD,
过点P作PE⊥AD于E,作PM⊥AB于M,
则四边形EAMP是矩形,
∴PM=PE=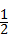 AB=2,
AB=2,
∵PM2=AM•BM=4,
∵AM+BM=4,
∴AM=2,
∴PA=2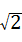 ,
,
同理可得P在P′时,PA=PB,
此时:PA=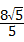 ;
;
∴当PA的长度等于2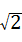 或
或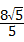 时,△PAD是等腰三角形;
时,△PAD是等腰三角形;
(2)过点P分别作PE⊥AB,PF⊥AD,垂足分别为E,F延长FP交BC于点G,
则PG⊥BC,
∵P点坐标为(a,b),
∴PE=b,PF=a,PG=4﹣a,
在△PAD,△PAB及△PBC中,
S1=2a,S2=2b,S3=8﹣2a,
∵AB为直径,
∴∠APB=90°,
∴PE2=AE•BE,
即b2=a(4﹣a),
∴2S1S3﹣S22=4a(8﹣2a)﹣4b2=﹣4b2+16a=﹣4(a﹣2)2+16,
∴当a=2时,b=2,2S1S3﹣S22有最大值16.

点评:此题考查了正方形的性质,圆周角的性质以及三角函数的性质等知识.此题综合性很强,解题时要注意数形结合与方程思想的应用.
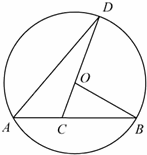
26、(2011•苏州)如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上的任意一点 (不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD.
(1)弦长等于 2 (结果保留根号);
(结果保留根号);
(2)当∠D=20°时,求∠BOD的度数;
(3)当AC的长度为多少时,以A、C、D为顶点的三角形与以B、C、0为顶点的三角形相似?请写出解答过程.
考点:圆周角定理;垂径定理;相似三角形的判定与性质;解直角三角形。
专题:几何综合题;数形结合。
分析:(1)过点O作OE⊥AB于E,由垂径定理即可求得AB的长;
(2)连接OA,由OA=OB,OA=OD,可得∠BAO=∠B,∠DAO=∠D,则可求得∠DAB的度数,又由圆周角等于同弧所对圆心角的一半,即可求得∠DOB的度数;
(3)由∠BCO=∠A+∠D,可得要使△DAC与△BOC相似,只能∠DCA=∠BCO=90°,然后由相似三角形的性质即可求得答案.
解答:解: 过点O作OE⊥AB于E,
过点O作OE⊥AB于E,
则AE=BE=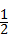 AB,∠OEB=90°,
AB,∠OEB=90°,
∵OB=2,∠B=30°,
∴BE=OB•cos∠B=2×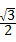 =
= ,
,
∴AB=2 ;
;
故答案为:2 ;
;
(2)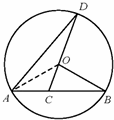 连接OA,
连接OA,
∵OA=OB,OA=OD,
∴∠BAO=∠B,∠DAO=∠D,
∴∠DAB=∠BAO+∠DAO=∠B+∠D,
又∵∠B=30°,∠D=20°,
∴∠DAB=50°,
∴∠BOD=2∠DAB=100°;
(3)∵∠BCO=∠A+∠D,
∴∠BCO>∠A,∠BCO>∠D,
∴要使△DAC与△BOC相似,只能∠DCA=∠BCO=90°,
此时∠BOC=60°,∠BOD=120°,
∴∠DAC=60°,
∴△DAC∽△BOC,
∵∠BCO=90°,
即OC⊥AB,
∴AC=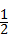 AB=
AB= .
.
点评:此题考查了垂径定理,圆周角的性质以及相似三角形的判定与性质等知识.题目综合性较强,解题时要注意数形结合思想的应用.
25、(2011•苏州)如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,巳知该山坡的坡度i(即tan∠ABC)为1: ,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.
,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.
(1)山坡坡角(即∠ABC)的度数等于 30 度;
(2)求A、B两点间的距离(结果精确到0.1米,参考数据: ≈1.732).
≈1.732).

考点:解直角三角形的应用-仰角俯角问题;解直角三角形的应用-坡度坡角问题。
分析:(1)根据俯角以及坡度的定义即可求解;
(2)在直角△PHB中,根据三角函数即可求得PB的长,然后在直角△PBA中利用三角函数即可求解.
解答:解:(1)30;
(2)由题意得:∠PBH=60°,∠APB=45°,
∵∠ABC=30°,
∴∠ABP=90°,
在直角△PHB中,PB=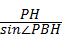 =20
=20 .
.
在直角△PBA中,AB=PB=20 ≈34.6米.
≈34.6米.
答:A,B两点间的距离是34.6米.
点评:本题主要考查了俯角的问题以及坡度的定义,正确利用三角函数是解题的关键.
24、(2011•苏州)如图所示的方格地面上,标有编号1、2、3的3个小方格地面是空地,另外6个小方格地面是草坪,除此以外小方格地面完全相同
(1)一只自由飞翔的小鸟,将随意地落在图中所示的方格地面上,求小鸟落在草坪上的概率;
(2)现准备从图中所示的3个小方格空地中任意选取2个种植草坪,则编号为1、2的2个小方格空地种植草坪的概率是多少 (用树状图或列表法求解)?

考点:列表法与树状图法;几何概率。
分析:根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.使用树状图分析时,一定要做到不重不漏.
解答:解:(1)P(小鸟落在草坪上)=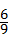 =
=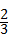 ;
;
(2)用树状图或列表格列出所有问题的可能的结果:
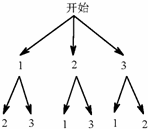
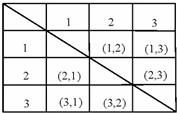
所以编号为1、2的2个小方格空地种植草坪的概率=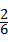 =
=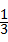 .
.
点评:此题主要考查了概率的求法:概率=所求情况数与总情况数之比.
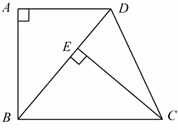
23、(2011•苏州)如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.
(1)求证:△ABD≌ECB;
(2)若∠DBC=50°,求∠DCE的度数.
考点:直角梯形;全等三角形的判定与性质。
分析:(1)因为这两个三角形是直角三角形,BC=BD,因为AD∥BC,还能推出∠ADB=∠EBC,从而能证明:△ABD≌ECB.
(2)因为∠DBC=50°,BC=BD,可求出∠BDC的度数,进而求出∠DCE的度数.
解答:解:(1)∵AD∥BC,
∴∠ADB=∠EBC.
∵CE⊥BD,∠A=90°,
∴∠A=∠CEB,
在△ABD和△ECB中,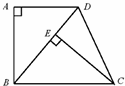
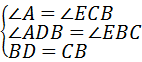
∴△ABD≌△ECB;
(2)∵∠DBC=50°,BC=BD,
∴∠EDC=65°,
又∵CE⊥BD,
∴∠CED=90°,
∴∠DCB=90°﹣∠EDC=25°.
点评:本题考查了全等三角形的判定和性质,以及直角梯形的性质,直角梯形有两个角是直角,有一组对边平行.
22、(2011•苏州)已知|a﹣1|+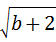 =0,求方裎
=0,求方裎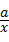 +bx=1的解.
+bx=1的解.
考点:解分式方程;非负数的性质:绝对值;非负数的性质:算术平方根。
专题:综合题;方程思想。
分析:首先根据非负数的性质,可求出a、b的值,然后再代入方程求解即可.
解答:解:∵|a﹣1|+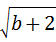 =0,
=0,
∴a﹣1=0,a=1;b+2=0,b=﹣2.
∴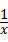 ﹣2x=1,得2x2+x﹣1=0,
﹣2x=1,得2x2+x﹣1=0,
解得x1=﹣1,x2=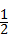 .
.
经检验:x1=﹣1,x2=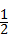 是原方程的解.
是原方程的解.
∴原方程的解为:x1=﹣1,x2=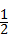 .
.
点评:本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.同时考查了解分式方程,注意解分式方程一定注意要验根.
21、(2011•苏州)先化简,再求值:(a﹣1+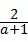 )÷(a2+1),其中a=
)÷(a2+1),其中a=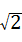 ﹣1.
﹣1.
考点:分式的化简求值。
分析:这道求分式值的题目,不应考虑把a的值直接代入,通常做法是先把分式通,把除法转换为乘法化简,然后再代入求值.
解答:解:原式=(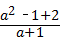 )•
)•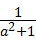 ,
,
=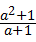 •
•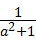 ,
,
=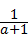 ,
,
当a=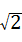 ﹣1时,
﹣1时,
原式=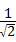 =
=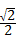 .
.
点评:此题主要考查了分式的计算,解答此题的关键是把分式化到最简,然后代值计算
20、(2011•苏州)解不等式:3﹣2(x﹣1)<1.
考点:解一元一次不等式。
分析:首先去括号,然后移项合并同类项,系数化为1,即可求解.
解答:解:3﹣2x+2<1,
得:﹣2x<﹣4,
∴x>2.
点评:本题考查了解简单不等式的能力,解答这类题学生往往在解题时不注意移项要改变符号这一点而出错.解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.
19、(2011•苏州)计算:22+|﹣1|﹣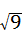 .
.
考点:实数的运算。
分析:此题涉及到乘方,绝对值,开方运算,针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
解答:解:原式=4+1﹣3=2.
点评:此题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握乘方、绝对值,开方等考点的运算.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com