
题目列表(包括答案和解析)
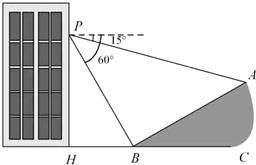
25、(2011•苏州)如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,巳知该山坡的坡度i(即tan∠ABC)为1: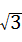 ,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.
,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.
(1)山坡坡角(即∠ABC)的度数等于 30 度;
(2)求A、B两点间的距离(结果精确到0.1米,参考数据: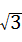 ≈1.732).
≈1.732).
考点:解直角三角形的应用-仰角俯角问题;解直角三角形的应用-坡度坡角问题。
分析:(1)根据俯角以及坡度的定义即可求解;
(2)在直角△PHB中,根据三角函数即可求得PB的长,然后在直角△PBA中利用三角函数即可求解.
解答:解:(1)30;
(2)由题意得:∠PBH=60°,∠APB=45°,
∵∠ABC=30°,
∴∠ABP=90°,
在直角△PHB中,PB=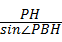 =20
=20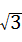 .
.
在直角△PBA中,AB=PB=20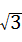 ≈34.6米.
≈34.6米.
答:A,B两点间的距离是34.6米.
点评:本题主要考查了俯角的问题以及坡度的定义,正确利用三角函数是解题的关键.
24、(2011•苏州)如图所示的方格地面上,标有编号1、2、3的3个小方格地面是空地,另外6个小方格地面是草坪,除此以外小方格地面完全相同
(1)一只自由飞翔的小鸟,将随意地落在图中所示的方格地面上,求小鸟落在草坪上的概率;
(2)现准备从图中所示的3个小方格空地中任意选取2个种植草坪,则编号为1、2的2个小方格空地种植草坪的概率是多少 (用树状图或列表法求解)?

考点:列表法与树状图法;几何概率。
分析:根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.使用树状图分析时,一定要做到不重不漏.
解答:解:(1)P(小鸟落在草坪上)=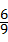 =
= ;
;
(2)用树状图或列表格列出所有问题的可能的结果:

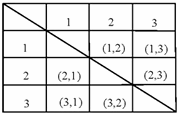
所以编号为1、2的2个小方格空地种植草坪的概率=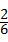 =
= .
.
点评:此题主要考查了概率的求法:概率=所求情况数与总情况数之比.
23、(2011•苏州)如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.
(1)求证:△ABD≌ECB;
(2)若∠DBC=50°,求∠DCE的度数.
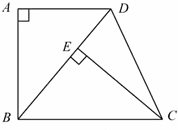
考点:直角梯形;全等三角形的判定与性质。
分析:(1)因为这两个三角形是直角三角形,BC=BD,因为AD∥BC,还能推出∠ADB=∠EBC,从而能证明:△ABD≌ECB.
(2)因为∠DBC=50°,BC=BD,可求出∠BDC的度数,进而求出∠DCE的度数.
解答:解:(1)∵AD∥BC,
∴∠ADB=∠EBC.
∵CE⊥BD,∠A=90°,
∴∠A=∠CEB,
在△ABD和△ECB中,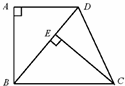
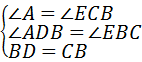
∴△ABD≌△ECB;
(2)∵∠DBC=50°,BC=BD,
∴∠EDC=65°,
又∵CE⊥BD,
∴∠CED=90°,
∴∠DCB=90°﹣∠EDC=25°.
点评:本题考查了全等三角形的判定和性质,以及直角梯形的性质,直角梯形有两个角是直角,有一组对边平行.
22、(2011•苏州)已知|a﹣1|+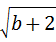 =0,求方裎
=0,求方裎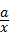 +bx=1的解.
+bx=1的解.
考点:解分式方程;非负数的性质:绝对值;非负数的性质:算术平方根。
专题:综合题;方程思想。
分析:首先根据非负数的性质,可求出a、b的值,然后再代入方程求解即可.
解答:解:∵|a﹣1|+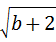 =0,
=0,
∴a﹣1=0,a=1;b+2=0,b=﹣2.
∴ ﹣2x=1,得2x2+x﹣1=0,
﹣2x=1,得2x2+x﹣1=0,
解得x1=﹣1,x2=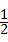 .
.
经检验:x1=﹣1,x2=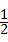 是原方程的解.
是原方程的解.
∴原方程的解为:x1=﹣1,x2=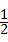 .
.
点评:本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.同时考查了解分式方程,注意解分式方程一定注意要验根.
21、(2011•苏州)先化简,再求值:(a﹣1+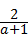 )÷(a2+1),其中a=
)÷(a2+1),其中a= ﹣1.
﹣1.
考点:分式的化简求值。
分析:这道求分式值的题目,不应考虑把a的值直接代入,通常做法是先把分式通,把除法转换为乘法化简,然后再代入求值.
解答:解:原式=(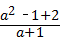 )•
)•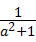 ,
,
=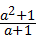 •
•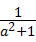 ,
,
=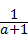 ,
,
当a= ﹣1时,
﹣1时,
原式= =
=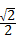 .
.
点评:此题主要考查了分式的计算,解答此题的关键是把分式化到最简,然后代值计算
20、(2011•苏州)解不等式:3﹣2(x﹣1)<1.
考点:解一元一次不等式。
分析:首先去括号,然后移项合并同类项,系数化为1,即可求解.
解答:解:3﹣2x+2<1,
得:﹣2x<﹣4,
∴x>2.
点评:本题考查了解简单不等式的能力,解答这类题学生往往在解题时不注意移项要改变符号这一点而出错.解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.
19、(2011•苏州)计算:22+|﹣1|﹣ .
.
考点:实数的运算。
分析:此题涉及到乘方,绝对值,开方运算,针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
解答:解:原式=4+1﹣3=2.
点评:此题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握乘方、绝对值,开方等考点的运算.
18、(2011•苏州)如图,已知点A的坐标为(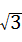 ,3),AB丄x轴,垂足为B,连接OA,反比例函数y=
,3),AB丄x轴,垂足为B,连接OA,反比例函数y=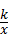 (k>0)的图象与线段OA、AB分别交于点C、D.若AB=3BD,以点C为圆心,CA的
(k>0)的图象与线段OA、AB分别交于点C、D.若AB=3BD,以点C为圆心,CA的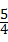 倍的长为半径作圆,则该圆与x轴的位置关系是 相交 (填”相离”,“相切”或“相交“).
倍的长为半径作圆,则该圆与x轴的位置关系是 相交 (填”相离”,“相切”或“相交“).
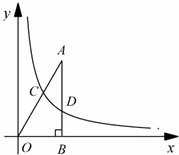
考点:直线与圆的位置关系;反比例函数图象上点的坐标特征。
分析:根据D点的坐标为(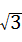 ,1),得出反比例函数y=
,1),得出反比例函数y=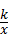 解析式,再根据A点坐标得出AO直线解析式,进而得出两图象的交点坐标,进而得出AC的长度,再利用直线与圆的位置关系得出答案.
解析式,再根据A点坐标得出AO直线解析式,进而得出两图象的交点坐标,进而得出AC的长度,再利用直线与圆的位置关系得出答案.
解答:解:∵已知点A的坐标为(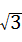 ,3),AB=3BD,
,3),AB=3BD,
∴AB=3,BD=1,
∴D点的坐标为(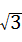 ,1),
,1),
∴反比例函数y=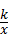 解析式为:
解析式为:
y=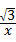 ,
,
∴AO直线解析式为:y=kx,
3=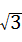 k,
k,
∴k=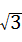 ,
,
∴y=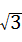 x,
x,
∴直线y=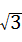 x与反比例函数y=
x与反比例函数y=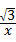 的交点坐标为:
的交点坐标为: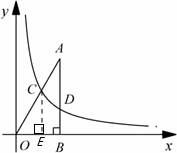
x=±1,
∴C点的横坐标为1,
纵坐标为: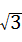 ,
,
CO=2,
∴AC=2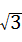 ﹣2,
﹣2,
∴CA的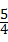 倍=
倍=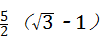 ,
,
CE=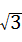 ,
,
∵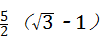 ﹣
﹣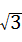 =
=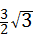 ﹣
﹣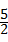 >0,
>0,
∴该圆与x轴的位置关系是相交.
故答案为:相交.
点评:此题主要考查了直线与圆的位置关系以及反比例函数的性质以及直线与反比例函数交点坐标的求法,综合性较强得出AC的长是解决问题的关键.
17、(2011•苏州)如图,巳知△ABC是面积为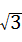 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于
的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于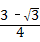 (结果保留根号).
(结果保留根号).
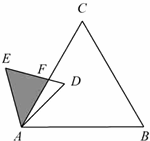
考点:相似三角形的性质;等边三角形的性质。
专题:计算题。
分析:根据相似三角形面积比等于相似比的平方求得三角形ADE的面积,再根据求出其边长,可根据三角函数得出三角形面积.
解答:解:∵△ABC∽△ADE,AB=2AD,
∴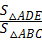 =
= ,
,
∵AB=2AD,S△ABC=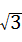 ,
,
∴S△ADE=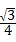 ,
,
在△EAD中,连接HF,则∠AFH=45°,∠EFH=30°,
设AH=HF=x,则EH=xtan30°=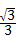 x.
x.
又∵S△ADE=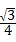 ,
,
∴AE=1,
∴x+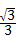 x=1,
x=1,
解得x=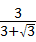 =
=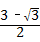 .
.
∴S△AEF=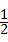 ×1×
×1×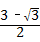 =
=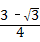 .
.
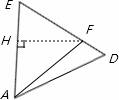
点评:此题主要考查相似三角形的判定与性质和等边三角形的性质等知识点,解得此题的关键是根据相似三角形面积比等于相似比的平方求得三角形ADE的面积,然后问题可解.
16、(2011•苏州)如图,巳知AB是⊙O的一条直径,延长AB至C点,使得AC=3BC,CD与⊙O相切,切点为D.若CD=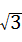 ,则线段BC的长度等于 1 .
,则线段BC的长度等于 1 .
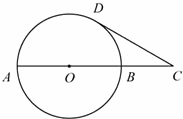
考点:切线的性质;勾股定理。
分析:根据切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项,即可求解.
解答:解:∵CD与⊙O相切,切点为D,
∴CD2=BC•AC,
即CD2=BC•3BC=3,
解得:BC=1.
故答案是:1.
点评:本题主要考查了切割线定理,正确理解定理是解题的关键.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com