
题目列表(包括答案和解析)
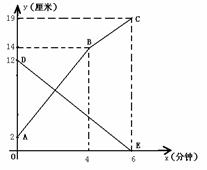
3. (2011江苏扬州,27,12分)如图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形块放其中(圆柱形铁块的下底面完全落在水槽底面上)现将甲槽中的水匀速注入乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分钟)之间的关系如图2所示。根据图象提供的信息,解答下列问题:
(1)图2中折线ABC表示 槽中的深度与注水时间之间的关系,线段DE表示 槽中的深度与注水时间之间的关系(以上两空选填“甲”、或“乙”),点B的纵坐标表示的实际意义是
(2)注水多长时间时,甲、乙两个水槽中的水的深度相同?
(3)若乙槽底面积为36平方厘米(壁厚不计),求乙槽中铁块的体积;
(4)若乙槽中铁块的体积为112立方厘米(壁厚不计),求甲槽底面积(直接写结果)。
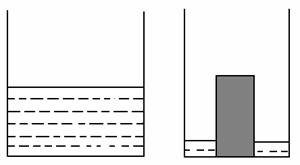
[答案]解:(1)乙,甲;乙槽内的圆柱形铁块的高度为14厘米。
(2)设线段AB的解析式为y1=kx+b,过点(0,2)、(4,14),可得解析式为y1=3x+2;
设线段DE的解析式为y2=mx+n,过点(0,12)、(6,0),可得解析式为y2=-2x+12;
当y1 =y2时,3x+2=-2x+12 ∴x=2。
(3)(19-14)×36=4×S甲 S甲 = 45 。
(4)60平方厘米。
理由如下:S铁=8
方程①:5S乙=4S甲
方程②:S乙×14=S甲×8+2×(S乙-8)+112
解得: S甲 = 60 ,S乙= 48.
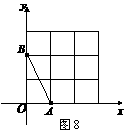
2. (2011福建福州,19,12分)
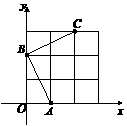
如图8,在平面直角坐标系中, 、
、 均在边长为1的正方形网格格点上.
均在边长为1的正方形网格格点上.
(1)求线段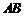 所在直线的函数解析式,并写出当
所在直线的函数解析式,并写出当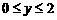 时,自变量
时,自变量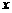 的取值范围;
的取值范围;
(2)将线段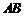 绕点
绕点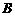 逆时针旋转
逆时针旋转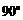 ,得到线段
,得到线段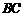 ,请在答题卡
,请在答题卡
指定位置画出线段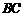 .若直线
.若直线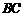 的函数解析式为
的函数解析式为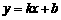 ,
,
则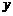 随
随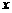 的增大而
(填“增大”或“减小”).
的增大而
(填“增大”或“减小”).

[答案](1)设直线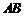 的函数解析式为
的函数解析式为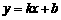
依题意,得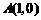 ,
,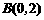
∴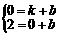
解得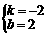
∴直线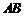 的函数解析式为
的函数解析式为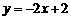
当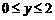 时,自变量
时,自变量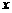 的取值范围是
的取值范围是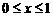 .
.
(2)线段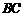 即为所求 增大
即为所求 增大

1. (2011浙江金华,22,10分)
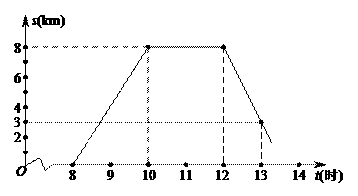
某班师生组织植树活动,上午8时从学校出发,到植树地点后原路返校,如图为师生离校路程s与时间t之间的图象.请回答下列问题:
(1)求师生何时回到学校?
(2)如果运送树苗的三轮车比师生迟半小时出发,与师生同路匀速前进,早半个小时到达植树地点,请在图中,画出该三轮车运送树苗时,离校路程s与时间t之间的图象,并结合图象直接写出三轮车追上师生时,离学校的路程;
(3)如果师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求14时前返回学校,往返平均速度分别为每小时10km、8km.现有A、B、C、D四个植树点与学校的路程分别是13km,15km、17km、19km,试通过计算说明哪几个植树点符合要求.
解:(1)设师生返校时的函数解析式为 ,
,
把(12,8)、(13,3)代入得,
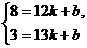 解得:
解得: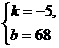
∴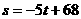 ,
,
当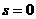 时,t=13.6 ,
时,t=13.6 ,
∴师生在13.6时回到学校;……3分
(2)图象正确2分.
由图象得,当三轮车追上师生时,离学校4km; ……2分
(3)设符合学校要求的植树点与学校的路程为x(km),由题意得:
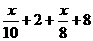 <14, 解得:x<
<14, 解得:x<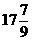 ,
,
答:A、B、C植树点符合学校的要求.……3分


7.
6. (2011江苏盐城,28,12分)如图,已知一次函数y = - x +7与正比例函数y = x的图象交于点A,且与x轴交于点B.
(1)求点A和点B的坐标;
(2)过点A作AC⊥y轴于点C,过点B作直线l∥y轴.动点P从原点O出发,以每秒1个单位长的速度,沿O-C-A的路线向点A运动;同时直线l从点B出发,以相同速度沿x轴向左平移,在平移过程中,直线l交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒.
①当t为何值时,以A、P、R为顶点的三角形的面积为8?
②是否存在以A、P、Q为顶点的三角形是等腰三角形?若存在,求t的值;若不存在,请说明理由.
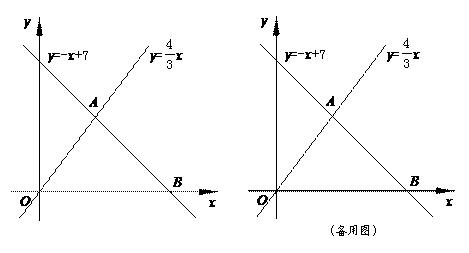

[答案](1)根据题意,得,解得 ,∴A(3,4) .
令y=-x+7=0,得x=7.∴B(7,0).
(2)①当P在OC上运动时,0≤t<4.

由S△APR=S梯形COBA-S△ACP-S△POR-S△ARB=8,得
(3+7)×4-×3×(4-t)- t(7-t)- t×4=8
整理,得t2-8t+12=0, 解之得t1=2,t2=6(舍)
当P在CA上运动,4≤t<7.
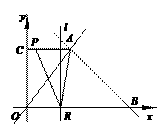
由S△APR= ×(7-t) ×4=8,得t=3(舍)
∴当t=2时,以A、P、R为顶点的三角形的面积为8.
②当P在OC上运动时,0≤t<4.
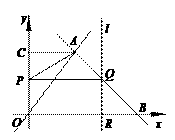
∴AP=,AQ=t,PQ=7-t
当AP =AQ时, (4-t)2+32=2(4-t)2,
整理得,t2-8t+7=0. ∴t=1, t=7(舍)
当AP=PQ时,(4-t)2+32=(7-t)2,
整理得,6t=24. ∴t=4(舍去)
当AQ=PQ时,2(4-t)2=(7-t)2
整理得,t2-2t-17=0 ∴t=1±3 (舍)
当P在CA上运动时,4≤t<7. 过A作AD⊥OB于D,则AD=BD=4.
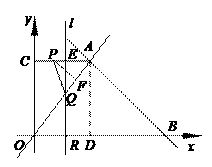
设直线l交AC于E,则QE⊥AC,AE=RD=t-4,AP=7-t.
由cos∠OAC= = ,得AQ = (t-4).
当AP=AQ时,7-t = (t-4),解得t = .
当AQ=PQ时,AE=PE,即AE= AP
得t-4= (7-t),解得t =5.
当AP=PQ时,过P作PF⊥AQ于F
AF= AQ = ×(t-4).
在Rt△APF中,由cos∠PAF= = ,得AF= AP
即 ×(t-4)= ×(7-t),解得t= .
∴综上所述,t=1或 或5或 时,△APQ是等腰三角形.
5. (2011浙江绍兴,21,10分)在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图中过点 分别作
分别作 轴,
轴, 轴的垂线,与坐标轴围成矩形
轴的垂线,与坐标轴围成矩形 的周长与面积相等,则点
的周长与面积相等,则点 是和谐点.
是和谐点.

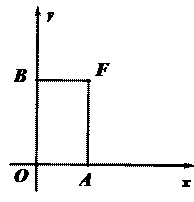
(1)判断点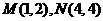 是否为和谐点,并说明理由;
是否为和谐点,并说明理由;
(2)若和谐点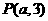 在直线
在直线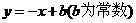 上,求点
上,求点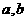 的值.
的值.
[答案](1)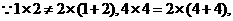
 点
点 不是和谐点,点
不是和谐点,点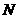 是和谐点.
是和谐点.
(2)由题意得,
当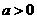 时,
时,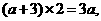
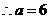 ,点
,点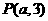 在直线
在直线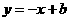 上,代入得
上,代入得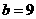 ;
;
当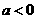 时,
时,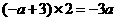
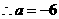 ,点
,点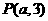 在直线
在直线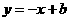 上,代入得
上,代入得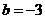 .
.
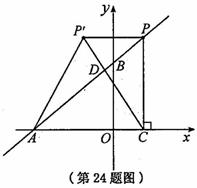
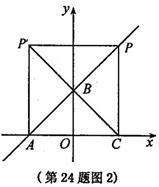
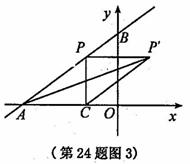
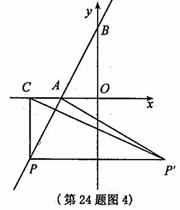
4. (2011浙江温州,24,14分)如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(-4,0),点B的坐标为(0,b)(b>0). P是直线AB上的一个动点,作PC⊥x轴,垂足为C.记点P关于y轴的对称点为P'(点P'不在y轴上),连结PP',P'A,P'C.设点P的横坐标为a.
(1)当b=3时,
①求直线AB的解析式;
②若点P'的坐标是(-1,m),求m的值;
(2)若点P在第一象限,记直线AB与P'C的交点为D. 当P'D:DC=1:3时,求a的值;
(3)是否同时存在a,b,使△P'CA为等腰直角三角形?若存在,请求出所有满足要求的a,b的值;若不存在,请说明理由.
[答案]解:(1)①设直线AB的解析式为y=kx+3,
把x=-4,y=0代人上式,得-4k+3=0,
∴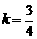 ,
,
∴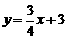
②由已知得点P的坐标是(1,m),
∴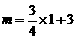 ,∴
,∴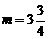 .
.
(2) ∵PP'∥AC,
∴△PP'D∽△ACB,
∴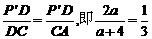 ,
,
∴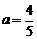 .
.
(3)以下分三种情况讨论.
①当点P在第一象限时,
i)若∠AP'C= 90°,P'A= P'C(如图1),过点P'作P'H⊥x轴于点'H,∴PP'=CH=AH=P'H
= AC,
AC,
∴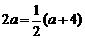 ,∴
,∴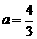 .
.
∵P'H=PC= AC,△ACP∽△AOB,
AC,△ACP∽△AOB,
∴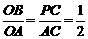 ,即
,即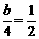 ,
,
∴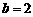 .
.
ii)若∠P'AC=90°,P'A= CA(如图2),则PP'=AC,∴2a=a+4,∴ a=4.
∵P'A=PC=AC, △ACP∽△AOB,
∴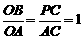 ,即
,即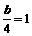 ,∴
,∴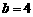 .
.
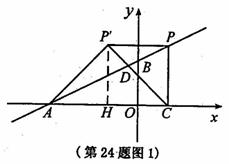
iii)若∠P'CA =90°,则点P',P都在第一象限,这与条件矛盾,
∴△P'CA不可能是以C为直角顶点的等腰直角三角形.
②当点P在第二象限时,∠P'CA为钝角(如图3),此时△P'CA不可能是等腰直角三角形.
③当点P在第三象限时,∠PAC为钝角(如图4), 此时△P'CA不可能是等腰直角三角形,∴所有满足条件的a,b的值为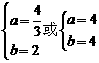 .
.
3. (2011浙江省,23,12分)设直线l1:y1=k1x+b1与l2:y2=k2x+b2,若l1⊥l2,垂足为H,则称直线l1与l2是点H的直角线.
(1) 已知直线①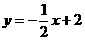 ;②
;②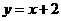 ;③
;③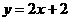 ;④
;④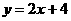 和点C(0,3).则直线
和 是点C的直角线(填序号即可);
和点C(0,3).则直线
和 是点C的直角线(填序号即可);
(2) 如图,在平面直角坐标系中,直角梯形OABC的顶点A(3,0)、B(2,7)、C(0,7),P为线段OC上一点,设过B、P两点的直线为l1,过A、P两点的直线为l2,若l1与 l2是点P的直角线,求直线l1与 l2的解析式.
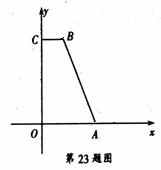
[答案](1)画图象可知,直线①与直线③是点C的直角线;(点C的坐标似乎有问题)
(2)设P坐标为(0,m),则PB⊥PB于点P。因此,AB2=(3-2)2+72=50,
又 ∵ PA2=PO2+OA2=m2+32,PB2=PC2+BC2=(7-m)2+22 ,
∴AB2=PA2+PB2=m2+32+(7-m)2+22=50
解得:m1=1,m2=6.
当m=1时,l1为:y1=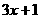 , l2为:y2=
, l2为:y2=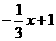 ;
;
当m=6时,l1为:y1=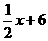 , l2为:y2=
, l2为:y2=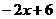 ;
;
2.
(2011
浙江湖州,19,6) 已知:一次函数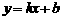 的图象经过M(0,2),(1,3)两点.
的图象经过M(0,2),(1,3)两点.
(l) 求k、b的值;
(2) 若一次函数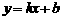 的图象与x轴的交点为A(a,0),求a的值.
的图象与x轴的交点为A(a,0),求a的值.
[答案](1)由题意得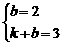 ,解得
,解得 ,∴k,b的值分别是1和2.
,∴k,b的值分别是1和2.
(2)由(1)得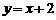 ,∴当y=0时,x=-2,即a=-2.
,∴当y=0时,x=-2,即a=-2.
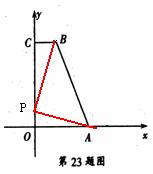
1. ((2011浙江杭州,17,6)点A,B,C,D的坐标如图,求直线AB与直线CD的交点坐标.
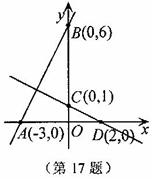
[答案]求直线AB和CD的解析式分别为: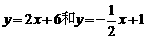 ,解方程组
,解方程组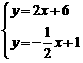 得:
得: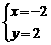 ,则直线AB与直线CD的交点坐标为
,则直线AB与直线CD的交点坐标为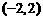 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com