
题目列表(包括答案和解析)
19.(1)5,36; (2分)
(2)420; (4分)
(3)以下两种方法任选一种
(用树状图)设平等、进取、和谐、感恩、互助的序号依次是①②③④⑤
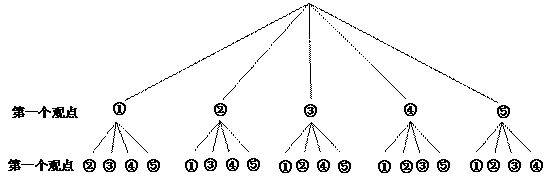
∴恰好选到“和谐”和“感恩”观点的概率是 (8分)
(用列表法)
|
|
平等 |
进取 |
和谐 |
感恩 |
互助 |
|
平等 |
|
平等、进取 |
平等、和谐 |
平等、感恩 |
平等、互助 |
|
进取 |
进取、平等 |
|
进取、和谐 |
进取、感恩 |
进取、互助 |
|
和谐 |
和谐、平等 |
和谐、进取 |
|
和谐、感恩 |
和谐、互助 |
|
感恩 |
感恩、平等 |
感恩、进取 |
感恩、和谐 |
|
感恩、互助 |
|
互助 |
互助、平等 |
互助、进取 |
互助、和谐 |
互助、感恩 |
|
∴恰好选到“和谐”和“感恩”观点的概率是 (8分)
18.解:
由①得:x<8 (2分)
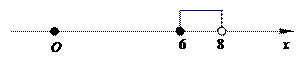 由②得x≥6
(4分)
由②得x≥6
(4分)
∴不等式的解集是:6≤x<8 (6分)
17.(1)解:原式=3´1–(2–)+(–1) (4分)
= (5分)
(2 )解: – = – (2分)
= = (4分)
当x = 时,∴原式= = (5分)
 (3)证明:∵平行四边形ABCD中,OA=OC,
(1分)
(3)证明:∵平行四边形ABCD中,OA=OC,
(1分)
由已知:AF=CE
AF–OA= CE – OC ∴OF=OE (3分)
同理得:OG=OH
∴四边形EGFH是平行四边形 (4分)
∴GF∥HE (5分)
9.(2x+1)(2x–1);10.2030、3150; 11.20°;12.– ;13.5π;14.2;15.20%;16.①②⑤.
24.(本小题满分12分)
已知抛物线的顶点是C (0,a) (a>0,a为常数),并经过点(2a,2a),点D(0,2a)为一定点.
(1)求含有常数a的抛物线的解析式;
(2)设点P是抛物线任意一点,过P作PH⊥x轴,垂足是H,求证:PD = PH;
 (3)设过原点O的直线l与抛物线在第一象限相交于A、B两点,若DA=2DB,且S△ABD = 4,求a的值.
(3)设过原点O的直线l与抛物线在第一象限相交于A、B两点,若DA=2DB,且S△ABD = 4,求a的值.
宜宾市2011年高中阶段学校招生考试
数学试题答案及评分意见
说明:
23.(本小题满分10分)
已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧上取一点E使∠EBC = ∠DEC,延长BE依次交AC于G,交⊙O于H.
(1)求证:AC⊥BH
(2)若∠ABC= 45°,⊙O的直径等于10,BD =8,求CE的长.

22.(本小题满分7分)
如图,飞机沿水平方向(A、B两点所在直线)飞行,前方有一座高山,为了避免飞机飞行过低,就必须测量山顶M到飞行路线AB的距离MN.飞机能够测量的数据有俯角和飞行的距离(因安全因素,飞机不能飞到山顶的正上方N处才测飞行距离),请设计一个距离MN的方案,要求:
(1)指出需要测量的数据(用字母表示,并在图中标出);
 (2)用测出的数据写出求距离MN的步骤.
(2)用测出的数据写出求距离MN的步骤.
21.(本小题满分7分)
如图,一次函数的图象与反比例函数y1= – ( x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0).当x<–1时,一次函数值大于反比例函数的值,当x>–1时,一次函数值小于反比例函数值.
(1)求一次函数的解析式;
(2) 设函数y2= (x>0)的图象与y1= – (x<0)的图象关于y轴对称.在y2= (x>0)的图象上取一点P(P点的横坐标大于2),过P作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
设函数y2= (x>0)的图象与y1= – (x<0)的图象关于y轴对称.在y2= (x>0)的图象上取一点P(P点的横坐标大于2),过P作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
20.(本小题满分7分)
某县为鼓励失地农民自主创业,在2010年对60位自主创业的失地农民自主创业的失地农民进行奖励,共计划奖励10万元.奖励标准是:失地农民自主创业连续经营一年以上的给予1000元奖励;自主创业且解决5人以上失业人员稳定就业一年以上的,再给予2000元奖励.问:该县失地农民中自主创业连续经营一年以上的和自主创业且解决5人以上失业人员稳定就业一年以上的农民分别有多少人?
19.(本小题8分)
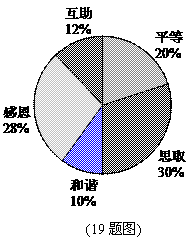
某校开展了以“人生观、价值观”为主题的班队活动,活动结束后,初三(2)班数学兴趣小组提出了5个主要观点并在本班50名学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图.
(1)该班学生选择“和谐”观点的有 人,在扇形统计图中,“和谐”观点所在扇形区域的圆心角是 度.
(2)如果该校有1500名初三学生,利用样本估计选择“感恩”观点的初三学生约有 人.
 (3)如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查,求恰好选到“和谐”和“感恩”观点的概率(用树状图或列表法分析解答)
(3)如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查,求恰好选到“和谐”和“感恩”观点的概率(用树状图或列表法分析解答)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com