
题目列表(包括答案和解析)
4、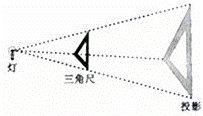 如图.位似图形由三角尺与其灯光照射下的中心投影组成,相似比为2:5,且三角尺的一边长为8cm,则投彩三角形的对应边长为( )B
如图.位似图形由三角尺与其灯光照射下的中心投影组成,相似比为2:5,且三角尺的一边长为8cm,则投彩三角形的对应边长为( )B
A、8cm B、20cm C、3.2cm D、10cm
考点:位似变换;中心投影.
专题:几何图形问题.
分析:根据位似图形的性质得出相似比为2:5,对应变得比为2:5,即可得出投彩三角形的对应边长.
解答:解:∵位似图形由三角尺与其灯光照射下的中心投影组成,相似比为2:5,三角尺的一边长为8cm,
∴投彩三角形的对应边长为:8÷ 25=20cm.
故选:B.
点评:此题主要考查了位似图形的性质以及中心投影的应用,根据对应变得比为2:5,再得出投彩三角形的对应边长是解决问题的关键.
3、将代数式x2+4x-1化成(x+p)2+q的形式( )C
A、(x-2)2+3 B、(x+2)2-4 C、(x+2)2-5 D、(x+2)2+4
考点:配方法的应用.
专题:配方法.
分析:根据配方法,若二次项系数为1,则常数项是一次项系数的一半的平方,若二次项系数不为1,则可先提取二次项系数,将其化为1后再计算.
解答:解:x2+4x-1=x2+4x+4-4-1=x+22-5,
故选C.
点评:本题考查了学生的应用能力,解题时要注意配方法的步骤,注意在变形的过程中不要改变式子的值,难度适中.
答题:
2、下列四个图案中,轴对称图形的个数是( )C

A、1 B、2 C、3 D、4
考点:轴对称图形.
分析:根据轴对称图形的定义1得出,图形沿一条直线对着,分成的两部分完全重合及是轴对称图形,分别判断得出即可.
解答:解:根据图象,以及轴对称图形的定义可得,
第1,2,4个图形是轴对称图形,第3个是中心对称图形,
故选:C.
点评:此题主要考查了轴对称图形的定义,根据定义判断出图形形状是解决问题的关键.
1、有理数- 12的倒数是( )B
A、-2 B、2 C、 12 D、- 12
考点:倒数.
专题:计算题.
分析:根据倒数的意义乘积为1的两个数互为倒数,用1除以 12可得.
解答:解:有理数- 12的倒数是:1÷(- 12)=-2.
故选B.
点评:此题考查的知识点为倒数,解答此题可根据倒数的意义乘积为1的两个数互为倒数,用1除以- 12可得.
24.(本题满分10分)孔明是一个喜欢探究钻 研的同学,他在和同学们一起研究某条抛物线
研的同学,他在和同学们一起研究某条抛物线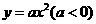 的性质时,将一把直角三角板的直角顶点置于平面直角坐标系的原点
的性质时,将一把直角三角板的直角顶点置于平面直角坐标系的原点 ,两直角边与该抛物线交
,两直角边与该抛物线交 于
于 、
、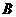 两点,请解答以下问题:
两点,请解答以下问题:
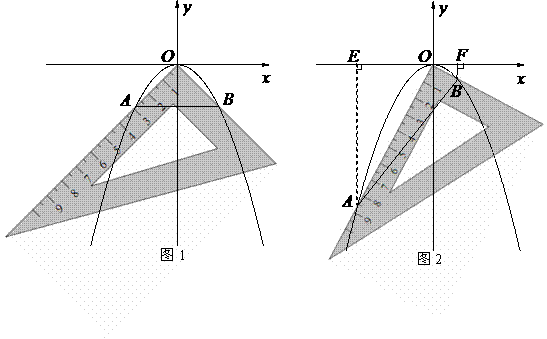
(1)若测得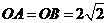 (如图1),求
(如图1),求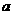 的值;
的值;
(2)对同一条抛物线,孔明将三角板绕点 旋转到如图2所示位置时,过
旋转到如图2所示位置时,过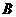 作
作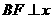 轴于点
轴于点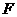 ,测得
,测得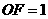 ,写出此时点
,写出此时点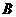 的坐标,并求点
的坐标,并求点 的横坐标;
的横坐标;
(3)对该抛物线,孔明将三角板绕点 旋转任意角度时惊奇地发现,交点
旋转任意角度时惊奇地发现,交点 、
、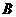 的连线段总经过一个固定的点,试说明理由并求出该点的坐标.
的连线段总经过一个固定的点,试说明理由并求出该点的坐标.
23.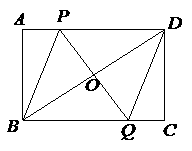 (本题满分8分)如图,矩形
(本题满分8分)如图,矩形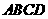 中,点
中,点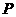 是线段
是线段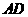 上一动点,
上一动点, 为
为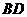 的中点,
的中点, 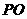 的延长线交
的延长线交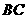 于
于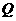 .
.
(1)求证: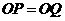 ;
;
(2)若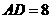 厘米,
厘米,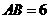 厘米,
厘米,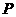 从点
从点 出发,
出发,
以1厘米/秒的速 度向
度向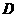 运动(不与
运动(不与
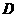 重合).
重合).
设点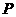 运动时
运动时 间为
间为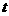 秒,请用
秒,请用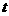 表示
表示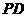 的长;
的长;
并求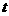 为何值时,四边形
为何值时,四边形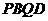 是菱形.
是菱形.
22.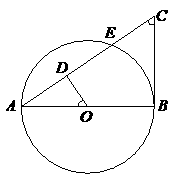 (本题满分8分)如图,
(本题满分8分)如图,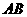 为
为 的直径,
的直径,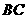 为
为 的切线,
的切线, 交
交 于点
于点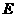 ,
,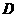 为
为 上一点,
上一点,
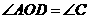 .
.
(1)求证: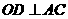 ;
;
(2)若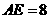 ,
,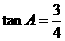 ,求
,求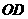 的长.
的长.
21.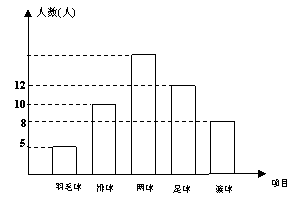 (本题满分6分)我国网球名将李娜在今年法国网球公开赛上的出色表现,大大激发了国人对网球的热情.在一项“你最喜欢的球类运动”的调查中,共有50名同学参与调查,每人必选且只选一项,将调查结果绘制成频数
(本题满分6分)我国网球名将李娜在今年法国网球公开赛上的出色表现,大大激发了国人对网球的热情.在一项“你最喜欢的球类运动”的调查中,共有50名同学参与调查,每人必选且只选一项,将调查结果绘制成频数 分布直方图如下,根据图中信息回答:
分布直方图如下,根据图中信息回答:
(1)被调查的同学中选择喜欢网球的有_ ___________________人;
___________________人;
(2)孔明同学在被调查中选择的是羽毛球,现要在参与调查选择喜 欢羽毛球的同学中随机抽取2人参加一项比赛,求孔明被选中的概率.
欢羽毛球的同学中随机抽取2人参加一项比赛,求孔明被选中的概率.
20.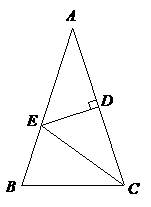 (本题满分6分)如图,
(本题满分6分)如图, 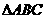 中,
中,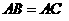 ,
,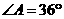 ,
, 的垂直平分线交
的垂直平分线交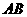 于
于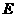 ,
,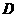 为垂足,连结
为垂足,连结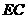 .
.
(1)求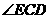 的度
的度 数;
数;
(2)若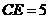 ,求
,求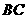 长.
长.
19.(本题满分6分)食品安全是老百姓关注的话题,在食品中添加过
量的添加剂对人体有害,但适量的添加剂对人体无害且有利于食品
的储存和运输.某饮料加工厂生产的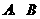 两种饮料均需加入同种
两种饮料均需加入同种
添加剂, 饮料每瓶需加该添加剂2克,
饮料每瓶需加该添加剂2克,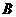 饮料每瓶需加该添加
饮料每瓶需加该添加
剂3克,已知270克该添加剂恰好生产了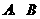 两种饮料共100瓶,问
两种饮料共100瓶,问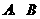 两种饮料各生产了多少瓶?
两种饮料各生产了多少瓶?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com