
题目列表(包括答案和解析)
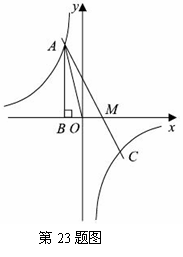
30. (2011贵州安顺,23,10分)如图,已知反比例函数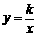 的图像经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB的面积为2.若直线y=ax+b经过点A,并且经过反比例函数
的图像经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB的面积为2.若直线y=ax+b经过点A,并且经过反比例函数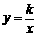 的图象上另一点C(n,一2).
的图象上另一点C(n,一2).
⑴求直线y=ax+b的解析式;
⑵设直线y=ax+b与x轴交于点M,求AM的长.

[答案](1)∵点A(-1,m)在第二象限内,∴AB = m,OB = 1,∴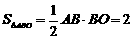
即: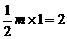 ,解得
,解得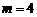 ,∴A (-1,4),
,∴A (-1,4),
∵点A (-1,4),在反比例函数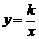 的图像上,∴4 =
的图像上,∴4 =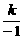 ,解得
,解得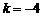 ,
,
∵反比例函数为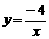 ,又∵反比例函数
,又∵反比例函数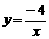 的图像经过C(n,
的图像经过C(n,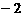 )
)
∴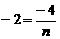 ,解得
,解得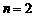 ,∴C (2,-2),
,∴C (2,-2),
∵直线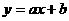 过点A (-1,4),C (2,-2)
过点A (-1,4),C (2,-2)
∴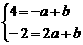 解方程组得
解方程组得 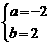
∴直线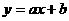 的解析式为
的解析式为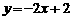 ;
;
(2)当y = 0时,即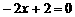 解得
解得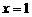 ,即点M(1,0)
,即点M(1,0)
在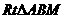 中,∵AB = 4,BM = BO +OM = 1+1 = 2,
中,∵AB = 4,BM = BO +OM = 1+1 = 2,
由勾股定理得AM=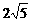 .
.
29. (2011重庆市潼南,23,10分)如图,
在平面直角坐标系中,一次函数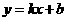 (k≠0)的图象与反比例函数
(k≠0)的图象与反比例函数
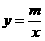 (m≠0)的图象相交于A、B两点.
(m≠0)的图象相交于A、B两点.
求:(1)根据图象写出A、B两点的坐标并分别求出反比例函数和一次函数的解析式;
(2)根据图象写出:当x为何值时,一次函数值大于反比例函数值.
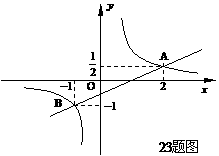
[答案]解:(1)由图象可知:点A的坐标为(2,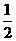 )
)
点B的坐标为(-1,-1) --------------2分
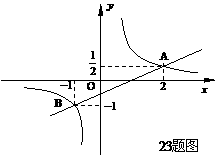
∵反比例函数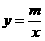 (m≠0)的图像经过点(2,
(m≠0)的图像经过点(2,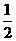 )
)
∴ m=1
 ∴反比例函数的解析式为:
∴反比例函数的解析式为: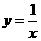 ---------------------4分
---------------------4分
∵一次函数y=kx+b(k≠0)的图象经过点(2,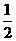 )点B(-1,-1)
)点B(-1,-1)
∴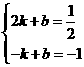
解得:k=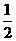 b=-
b=-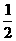
∴一次函数的解析式为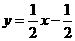 ----------------------6分
----------------------6分
(2)由图象可知:当x>2 或 -1<x<0时一次函数值大于反比例函数值 --------10分
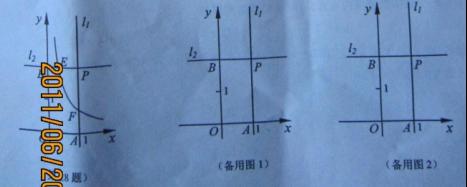
28. (20011江苏镇江,28,10分)在平面直角坐标系xOy中,直线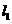 过点A(1,0)且与y轴平行,直线
过点A(1,0)且与y轴平行,直线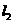 过点B(0,2)且与x轴平行,直线
过点B(0,2)且与x轴平行,直线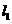 与
与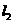 相交于P.点E为直线
相交于P.点E为直线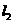 一点,反比例函数
一点,反比例函数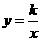 (k>0)的图象过点E且与直线
(k>0)的图象过点E且与直线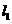 相交于点F.
相交于点F.
(1)若点E与点P重合,求k的值;
(2)连接OE、OF、EF.若k>2,且△OEF的面积为△PEF的面积2倍,求点E的坐标;
(3)是否存在点E及y轴上的点M,使得以点M、E、F为顶点的三角形与△PEF全等?若存在,求点E的坐标;若不存在,请说明理由.
[答案]
(1)k=1×2=2.
(2)当k>2时,如图,点E、F分别在P点的右侧和上方过E作x轴的垂线EC,垂足为C,过F作y轴的垂线FD,垂足为D,EC和FD相交于G,则四边形OCGD为矩形。
∵ PF⊥PE.
∴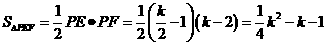
四边形OCGD为矩形
∴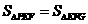
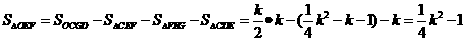
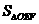 =2
=2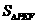
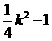 =
=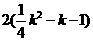
解得k=6或2.因为k=2时,E、F重合,所以k=6.
所以E点的坐标为(3,2)
(3)存在点E及y轴上的点M,使得△MEF与△PEF全等
①当k<2时,如图,只可能△MEF≌△PEF。

作FH⊥y轴于H,
△FHM∽△MBE得: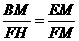 .
.
∵FH=1,EM=PE=1-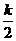 ,FM=PF=2-k
,FM=PF=2-k
∴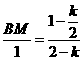 ,BM=
,BM=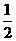 ,
,
在Rt△MBE中,由勾股定理得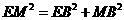 ,
,
∴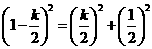 ,解得k=
,解得k=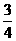 ,此时E点的坐标为(
,此时E点的坐标为(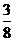 ,2)
,2)
②当k>2时,如图
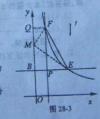
只可能只可能△MEF≌△PEF,作作FQ⊥y轴于Q,
△FQM∽△MBE得: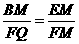
∵FQ=1,EM=PF=k-2,FM=PE=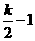 ,
,
∴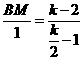 ,BM=2,
,BM=2,
在Rt△MBE中,由勾股定理得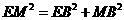 ,
,
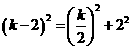
解得k=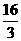 或0,但k=0不符合题意,所以k=
或0,但k=0不符合题意,所以k=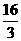 。
。
此时E点的坐标为(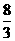 ,2),符合条件的E点坐标为
,2),符合条件的E点坐标为
(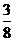 ,2)和(
,2)和(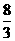 ,2)。
,2)。
27. (2011湖北襄阳,18,5分)
已知直线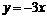 与双曲线
与双曲线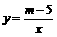 交于点P(-1,n).
交于点P(-1,n).
(1)求m的值;
(2)若点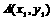 ,
,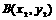 在双曲线
在双曲线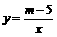 上,且
上,且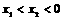 ,试比较
,试比较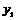 ,
,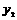 的大小.
的大小.
[答案]
(1)∵点P(-1,n)在直线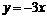 上,∴
上,∴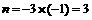 .····· 1分
.····· 1分
∵点P(-1,n)在双曲线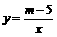 上,∴
上,∴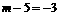 ,即m=2. ·· 3分
,即m=2. ·· 3分
(2)∵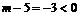 ,∴当x<0时,y随x的增大而增大
,∴当x<0时,y随x的增大而增大
又∵点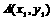 ,
,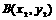 在双曲线
在双曲线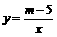 上,且
上,且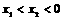 ,
,
∴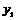 <
<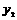 . 5分
. 5分
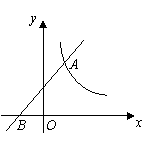
26. (2011广东肇庆,23,8分)如图,一次函数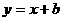 的图象经过点B(
的图象经过点B(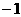 ,0),且与反比例函数
,0),且与反比例函数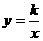 (
(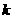 为不等于0的常数)的图象在第一象限交于点
为不等于0的常数)的图象在第一象限交于点 (1,
(1,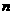 ).求:
).求:
(1)一次函数和反比例函数的解析式;
(2)当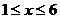 时,反比例函数
时,反比例函数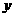 的取值范围.
的取值范围.

[答案]解:(1)将点B(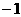 ,0)代入
,0)代入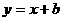 得:
得: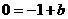 ∴b=1.
∴b=1.
∴一次函数的解析式是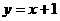
∵点 (1,
(1,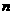 )在一次函数
)在一次函数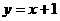 的图象上,将点
的图象上,将点 (1,
(1,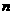 )代入
)代入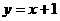 得:
得:
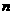 =1+1,∴
=1+1,∴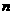 =2
=2
即点 的坐标为(1,2),代入
的坐标为(1,2),代入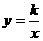 得:
得: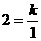 ,解得:
,解得: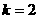
∴反比例函数的解析式是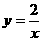
(2)对于反比例函数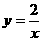 ,当
,当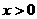 时,
时,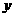 随
随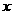 的增大而减少,
的增大而减少,
而当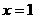 时,
时,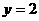 ;当
;当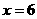 时,
时,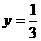
∴当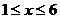 时,反比例函数
时,反比例函数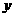 的取值范围是
的取值范围是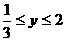
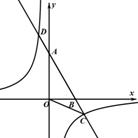
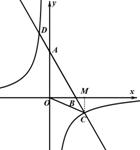
25. (2011湖南衡阳,25,8分)如图,已知A,B两点的坐标分别为A(0,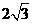 ),B(2,0)直线AB与反比例函数
),B(2,0)直线AB与反比例函数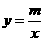 的图像交与点C和点D(-1,a).
的图像交与点C和点D(-1,a).
(1)求直线AB和反比例函数的解析式;
(2)求∠ACO的度数;
(3)将△OBC绕点O逆时针方向旋转 α角(α为锐角),得到△OB′C′,当α为多少度时OC′⊥AB,并求此时线段AB′的长.
α角(α为锐角),得到△OB′C′,当α为多少度时OC′⊥AB,并求此时线段AB′的长.
[解](1)设直线AB的解析式为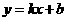 ,将A(0,
,将A(0,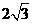 ),B(2,0)代入解析式
),B(2,0)代入解析式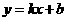 中,得
中,得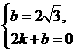 ,解得
,解得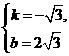 .∴直线AB的解析式为
.∴直线AB的解析式为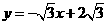 ;将D(-1,a)代入
;将D(-1,a)代入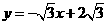 得
得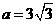 ,∴点D坐标为(-1,
,∴点D坐标为(-1,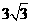 ),将D(-1,
),将D(-1,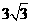 )代入
)代入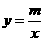 中得
中得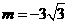 ,∴反比例函数的解析式为
,∴反比例函数的解析式为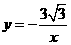 .
.
(2)解方程组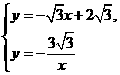 得
得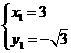 ,
,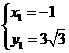 ,∴点C坐标为(3,
,∴点C坐标为(3,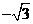 ),
),
过点C作CM⊥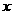 轴于点M,则在Rt△OMC中,
轴于点M,则在Rt△OMC中,
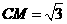 ,
,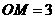 ,∴
,∴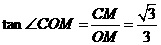 ,∴
,∴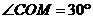 ,
,
在Rt△AOB中,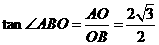 =
=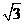 ,∴
,∴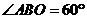 ,
,
∴∠ACO= .
.
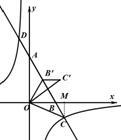
(3)如图,∵OC′⊥AB,∠ACO=30°,
∴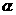 = ∠COC′=90°-30°=60°,∠BOB′=
= ∠COC′=90°-30°=60°,∠BOB′=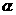 =60°,
=60°,
∴∠AOB′=90°-∠BOB′=30°,∵ ∠OAB=90°-∠ABO=30°,
∴∠AOB′=∠OAB,
∴AB′= OB′=2.
答:当α为60度时OC′⊥AB,并求此时线段AB′的长为2.
24. (2011四川绵阳,21,12)右图中曲线是反比例函数y=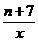 的图像的一支。
的图像的一支。
(1)这个反比例函数图象的另一支位于哪个象限?常数n的取值范围是什么?
(2)若一次函数y=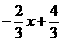 的图像与反比例函数图像交于点A,与x交于B,△AOB的面积为2,求n的值。
的图像与反比例函数图像交于点A,与x交于B,△AOB的面积为2,求n的值。
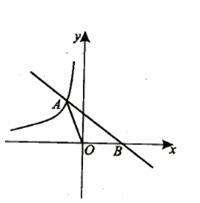
[答案](1)第四象限,n<-7
(2)∵y=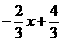
与x轴的交点是y=0,∴B点坐标为(2,0)又∵△AOB面积是2 ,∴A点纵坐标是2,代入y=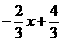
可得A点横从标是-1,所以n+7= -2,n= -9
23. (2011山东临沂,24,10分)如图,一次函数y=kx+b与反比例函数y=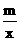 的图象交于A(2,3),B(-3,n)两点.
的图象交于A(2,3),B(-3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>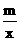 的解集______________;
的解集______________;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.
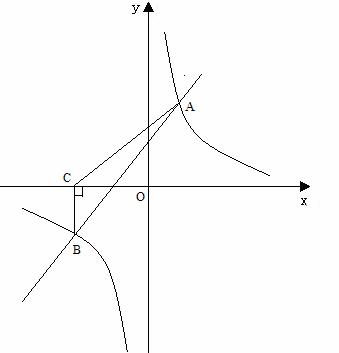
[解](1)∵点A(2,3)在y=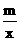 的图象上,
的图象上,
∴m=6,……………………………………………………………………………( 1分)
∴反比例函数的解析式为y=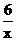 ,
,
∴n=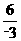 =-2,……………………………………………………………………(2分)
=-2,……………………………………………………………………(2分)
∵点A(2,3),B(-3,-2)在y=kx+b的图象上,
∴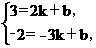
∴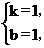
∴一次函数的解析式为y=x+1.…………………………………………………(4分)
(2)-3<x<0或x>2;……………………………………………………………(7分)
(3)方法一:设AB交x轴于点D,则D的坐标为(-1,0),
∴CD=2,………………………………………………………………………( 8分)
∴S△ABC=S△BCD+S△ACD
=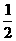 ×2×2+
×2×2+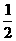 ×2×3=5.……………………………………………( 10分)
×2×3=5.……………………………………………( 10分)
方法二:以BC为底,则BC边上的高为3+2=5,…………………( 8分)
∴S△ABC=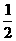 ×2×5=5.………………………………………………( 10分)
×2×5=5.………………………………………………( 10分)
22. (2011江苏南通,28,14分)(本小题满分14分)
如图,直线l经过点A(1,0),且与双曲线y=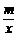 (x>0)交于点B(2,1),过点P(p,p-1)(p>1)作x轴的平行线分别交曲线y=
(x>0)交于点B(2,1),过点P(p,p-1)(p>1)作x轴的平行线分别交曲线y=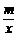 (x>0)和y=-
(x>0)和y=-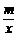 (x<0)于M,N两点.
(x<0)于M,N两点.
(1)求m的值及直线l的解析式;
(2)若点P在直线y=2上,求证:△PMB∽△PNA;
(3)是否存在实数p,使得S△AMN=4S△APM?若存在,请求出所有满足条件的p的值;若不存在,请说明理由.
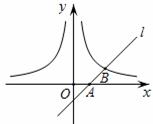
[答案](1)∵点B(2,1)在双曲线y=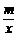 上,
上,
∴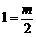 ,得m=2.
,得m=2.
设直线l的解析式为y=kx+b
∵直线l过A(1,0)和B(2,1)
∴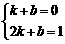 ,解得
,解得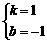
∴直线l的解析式为y=x-1.
(2) 证明:当x=p时,y=p-1,点P(p,p-1)(p>1)
在直线l上,如图.
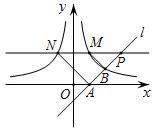
∵P(p,p-1)(p>1)在直线y=2上,
∴p-1=2,解得p=3
∴P(3,2)
∵PN∥x轴,∴P、M、N的纵坐标都等于2
把y=2分别代入双曲线y=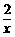 和y=
和y=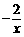 ,得M(1,2),N(-1,2)
,得M(1,2),N(-1,2)
∴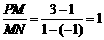 ,即M是PN的中点,
,即M是PN的中点,
同理:B是PA的中点,
∴BM∥AN
∴△PMB∽△PNA.
(3)由于PN∥x轴,P(p,p-1)(p>1),
∴M、N、P的纵坐标都是p-1(p>1)
把y=p-1分别代入双曲线y=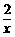 (x>0)和y=-
(x>0)和y=-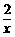 (x<0),
(x<0),
得M的横坐标x=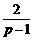 和N的横坐标x=-
和N的横坐标x=-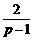 (其中p>1)
(其中p>1)
∵S△AMN=4S△APM且P、M、N在同一直线上,
∴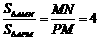 ,得MN=4PM
,得MN=4PM
即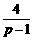 =4(p-
=4(p-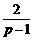 ),整理得:p2-p-3=0,
),整理得:p2-p-3=0,
解得:p=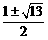
由于p>1,∴负值舍去
∴p=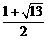
经检验p=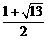 是原题的解,
是原题的解,
∴存在实数p,使得S△AMN=4S△APM,
p的值为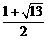 .
.
21. (2011江西南昌,19,6分)如图,四边形ABCD为菱形,已知A(0,4),B(-3,0)。
⑴求点D的坐标;
⑵求经过点C的反比例函数解析式.
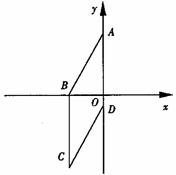
[答案](1)根据题意得AO=4,BO=3,∠AOB=90°,
所以AB=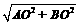 =
=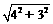 =5.
=5.
因为四边形ABCD为菱形,所以AD=AB=5,
所以OD=AD-AO=1,
因为点D在y轴负半轴,所以点D的坐标为(-1,0).
(2)设反比例函数解析式为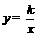 .
.
因为BC=AB=5,OB=3,
所以点C的坐标为(-3,-5).
因为反比例函数解析式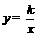 经过点C,
经过点C,
所以反比例函数解析式为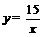 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com