
题目列表(包括答案和解析)
26.(本题满分10分)利民商店经销甲、乙两种商品. 现有如下信息:
 请根据以上信息,解答下列问题:
请根据以上信息,解答下列问题:
(1)甲、乙两种商品的进货单价各多少元?
(2)该商店平均每天卖出甲商品500件和乙商品300件.经调查发现,甲、乙两种商品
零售单价分别每降0.1元,这两种商品每天可各多销售100件.为了使每天获取更大的利润,商店决定把甲、乙两种商品的零售单价都下降m元. 在不考虑其他因素的条件下,当m定为多少时,才能使商店每天销售甲、乙两种商品获取的利润最大?每天的最大利润是多少?
[答案](1)设甲商品的进货单价是x元,乙商品的进货单价是y元.
根据题意,得 解得
答:甲商品的进货单价是2元,乙商品的进货单价是3元.
(2)设商店每天销售甲、乙两种商品获取的利润为s元,则
s=(1-m)(500+100×)+(2-m)(300+100×)
即 s=-2000m2+2200m+1100 =-2000(m-0.55)2+1705.
∴当m=0.55时,s有最大值,最大值为1705.
答:当m定为0.55时,才能使商店每天销售甲、乙两种商品获取的利润最大,每
天的最大利润是1705元.
[考点]根据等量关系列方程组种函数关系式,二次函数的最大值。
[分析](1)根据信息1:甲、乙两种商品的进货单价之和是5元;易列第一个方程x+y=5 。
根据信息2:甲商品零售单价比进货单价多1元,乙商品零售单价比进货单价的2倍少1元
知道甲商品零售单价为x+1,乙商品零售单价为2y-1,根据信息3:按零售单价购买甲商品3件和乙商品2件,共付了19元.列第二个方程3(x+1)+2(2y-1)=19。联立求解即可。
(2)根据利润=销售收入-销售成本公式 甲种商品的销售收入为:(3-m)(500+100×),销售成本为:2(500+100×),利润为(1-m)(500+100×)。乙种商品的销售收入为:(5-m)(300+100×),销售成本为:3(300+100×),利润为(2-m)(300+100×)。从而列出函数式,化为s=-a(m-b)2+c的形式.求出m=b时,s有最大利润c。
25. (本题满分10分)如图,在△ABC中,∠C= 90°,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.
(本题满分10分)如图,在△ABC中,∠C= 90°,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.
(1)若AC=6,AB= 10,求⊙O的半径;
(2)连接OE、ED、DF、EF.若四边形BDEF是平行四边形,试判断四边形OFDE的形状,并说明理由.
[答案]解:(1)连接OD. 设⊙O的半径为r.
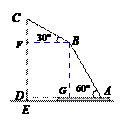
∵BC切⊙O于点D,∴OD⊥BC. 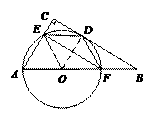
∵∠C=90°,∴OD∥AC,∴△OBD∽△ABC.
∴ = ,即 = . 解得r = ,
∴⊙O的半径为.
(2)四边形OFDE是菱形.
∵四边形BDEF是平行四边形,∴∠DEF=∠B.
∵∠DEF=∠DOB,∴∠B=∠DOB.
∵∠ODB=90°,∴∠DOB+∠B=90°,∴∠DOB=60°.
∵DE∥AB,∴∠ODE=60°.∵OD=OE,∴△ODE是等边三角形.
∴OD=DE.∵OD=OF,∴DE=OF.∴四边形OFDE是平行四边形.
∵OE=OF,∴平行四边形OFDE是菱形.
[考点]直线与圆相切的性质,相似三角形的判定和性质,平行四边形的性质,同弧所对的圆同角与圆心角的关系,直角三角形两锐角的关系,菱形的判定。
[分析](1)要求⊙O的半径,就要把它放到三角形内,故作辅助线:连接OD。这样△OBD和△ABC易证相似,再用对应边的比就可求出半径。
(2)要证四边形OFDE是菱形,由于OE和OF都是半径,故只要证四边形OFDE是平行四边形即可。要证这一点,由于四边形BDEF是平行四边形,有DE∥BF(ED∥OF),故只要证DE=OF,这一点由同弧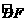 所对的圆同角∠DEF等于圆心角∠DOB的一半,平行四边形对角相等∠DEF=∠B和直角三角形两锐角互余∠DOB+∠B=90°容易得到。
所对的圆同角∠DEF等于圆心角∠DOB的一半,平行四边形对角相等∠DEF=∠B和直角三角形两锐角互余∠DOB+∠B=90°容易得到。
24. (本题满分10分)如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°. 使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?(结果精确到0.1cm,参考数据:≈1.732)
(本题满分10分)如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°. 使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?(结果精确到0.1cm,参考数据:≈1.732)
 [答案]解:过点B作BF⊥CD于F,作BG⊥AD于G.
[答案]解:过点B作BF⊥CD于F,作BG⊥AD于G.
在Rt△BCF中,∠CBF=30°,∴CF=BC·sin30°= 30× =15.
在Rt△ABG中,∠BAG=60°,∴BG=AB·sin60°= 40× = 20.
∴CE=CF+FD+DE=15+20+2=17+20≈51.64≈51.6(cm)cm.
答:此时灯罩顶端C到桌面的高度CE约是51.6cm.
[考点]解直角三角形,特殊角直角三角形值,矩形性质。
[分析]要求CE就要考虑三角形,所以作辅助线:过点B作BF⊥CD于F,作BG⊥AD于G. 得到两个直角三角形和一个矩形。这样利用解直角三角形就易求出。
23.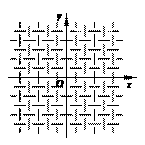 (本题满分10分)已知二次函数y = - x2 - x + .
(本题满分10分)已知二次函数y = - x2 - x + .
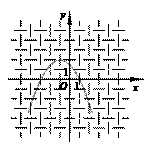
(1)在给定的直角坐标系中,画出这个函数的图象;
(2)根据图象,写出当y < 0时,x的取值范围;
(3)若将此图象沿x轴向右平移3个单位,请写出
 平移后图象所对应的函数关系式.
平移后图象所对应的函数关系式.
[答案]解:(1)画图(如图);
(2)当y < 0时,x的取值范围是x<-3或x>1;
(3)平移后图象所对应的函数关系式为y=- (x-2)2+2
[考点]二次函数,平移。
[分析](1)∵y = - x2 - x + =- (x+1)2+2;y=0,x=-2,1。
∴这个函数的图象顶点在(-1,2),对称轴是x=-1,与x轴的两个交点是
(-2,0),(1,0)。据此可画出这个函数的图象。
(2)根据图象,y < 0时图象在x轴下方,此时对应的x的取值范围是x<-3或
x>1。
(3)若将此图象沿x轴向右平移3个单位,只要考虑图象顶点(-1,2)向右平移3个单位得到(3,2),从而由y=- (x+1)2+2变为y=- (x-2)2+2。
22. (本题满分8分)为迎接建党90周年,某校组织了以“党在我心中”为主题的电子
(本题满分8分)为迎接建党90周年,某校组织了以“党在我心中”为主题的电子
小报制作比赛,评分结果只有60,70,80,90,100五种.现从中随机抽取部分作品,对
其份数及成绩进行整理,制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)求本次抽取了多少份作品,并补全两幅统计图;
(2)已知该校收到参赛作品共900份,请估计该校学生比赛成绩达到90分以上(含90分)的作品有多少份?
[答案]解:(1)∵24÷20%=120(份),∴本次抽取了120份作品.
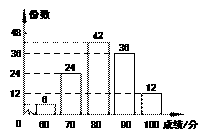
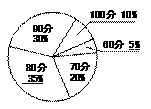 补全两幅统计图
补全两幅统计图
(2)∵900×(30%+10%)=360(份);
∴估计该校学生比赛成绩达到90分以上(含90分)的作品有360份.
[考点]统计图表分析。
[分析]统计图表的分析。
21.(本题满分8分)小明有3支水笔,分别为红色、蓝色、黑色;有2块橡皮,分别为
白色、灰色.小明从中任意取出1支水笔和1块橡皮配套使用.试用树状图或表格列出所有
可能的结果,并求取出红色水笔和白色橡皮配套的概率.
[答案]解:解法一:画树状图:
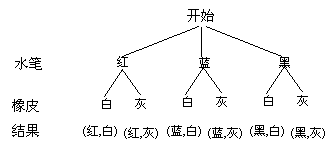
P(红色水笔和白色橡皮配套)= .
解法二:用列表法:
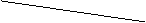 
|
白 |
灰 |
||||||
|
红 |
(红,白) |
(红,灰) |
||||||
|
蓝 |
(蓝,白) |
(蓝,灰) |
||||||
|
黑 |
(黑,白) |
(黑,灰) |
P(红色水笔和白色橡皮配套)= .
[考点]概率,树状图或列表法。
[分析]用树状图或列表法列举出所有情况,并找取出红色水笔和白色橡皮配套的情况数,求出概率.
20.(本题满分8分)解不等式组并把解集在数轴上表示出来.
[答案]解:解不等式<1,得x<1;
解不等式2(1-x)≤5,得x≥-;
 ∴原不等式组的解集是- ≤x<1.
∴原不等式组的解集是- ≤x<1.
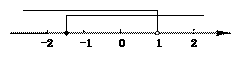
解集在数轴上表示为
[考点]一元一次不等式组,数轴。
[分析]根据一元一次不等式组的求解方法直接求解 。
19.(本题满分8分)
(1)计算:( )0 - ( )-2 + tan45°;
[答案]解:原式=1-4+1=-2.
[考点]零次幂,负指数幂,特殊角直角三角形值。
[分析]根据零次幂、负指数幂定义和特殊角直角三角形值直接求解。
(2)解方程: - = 2.
[答案]解:去分母,得 x+3=2(x-1) . 解之,得x=5. 经检验,x=5是原方程的解.
[考点]分式方程。
[分析]根据分式方程的求解方法直接求解 。
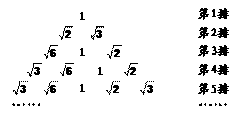
18.将1、、、按右侧方式排列.若规定
(m,n)表示第m排从左向右第n个数,则(5,4)
与(15,7)表示的两数之积是 ▲ .
[答案]2。
[考点]分类、归纳思想,根式计算。
[分析](5,4)从右侧可见为。下面求(15,7)是几:首先看(15,7)是整个排列的
第几个数,从排列方式看第1排1个数,第2排2个数,……第m排m个数,所以前14
排一共的数目是1+2+……+14=(1+14)+(2+13)+……+(7+8)=7×15=105,因此(15,7)
是第105+7=112个数。第二看第112个数是哪个数,因为112/4商余0,所以(15,7)=。
则(5,4)与(15,7)表示的两数之积是×=2。
17.如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.
以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路长
为 ▲ cm.
[答案]π。
[考点]旋转变形,,扇形弧长。
[分析]当△ADE按顺时针方向旋转到△ABF时,点E所经过的路长是一个以点A为圆心,
AE为半径,圆心角为900的。而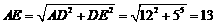 ,故点E所经过的路长
,故点E所经过的路长
 为
为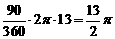 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com