
题目列表(包括答案和解析)
8. (2011浙江温州,21,10分)一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同.
(1)求摸出1个球是白球的概率;
(2)摸出1个球,记下颜色后放回,并搅匀,再摸出1个球,求两次摸出的球恰好颜色不同的概率(要求画树状图或列表);
(3)现再将n个白球放入布袋,搅匀后,使摸出1个球是白球的概率为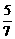 ,求n的值.
,求n的值.
[答案] 解:(1)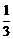
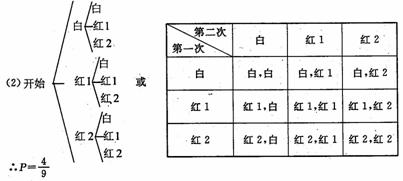
(3)由题意得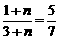 ,∴
,∴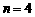
经检验,n=4是所列方程的根,且符合题意.
7. (2011浙江衢州,20,6分)
研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球于黄球.这样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,在进行摸球实验.摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中再继续.
活动结果:摸球实验活动一共做了50次,同级结果如下表:
|
球的颜色 |
无记号 |
有记号 |
||
|
红色 |
黄色 |
红色 |
黄色 |
|
|
摸到的次数 |
18 |
28 |
2 |
2 |
推测计算:有上述的摸球实验可推算:
盒中红球、黄球各占总球数的百分比分别是多少?
盒中有红球多少个?
[答案]解:(1)由题意可知;50次摸球实验活动中,出现红球20次,黄球30次,
所以红球所占百分比为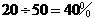
黄球所占百分比为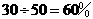
答:红球占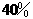 黄球占
黄球占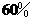
(2)由题意可知,50次摸球实验活动中,出现有记号的球4次,所以总球数为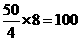 。所以红球数为
。所以红球数为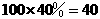 。答:盒中红球有40个。
。答:盒中红球有40个。
6. (2011宁波市,20,6分)在一个不透明的袋子中装有3个除颜色外完全相同的小球,其中白球1个,黄球1个,红球1个,摸出一个球记下颜色后放回,再摸出一个球,请用列表或树形图法求两次都摸到红球的概率.
[答案]解:树形图如下:
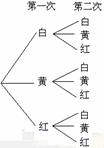
列表如下:
|
|
白 |
黄 |
红 |
|
白 |
白白 |
白黄 |
白红 |
|
黄 |
黄白 |
黄黄 |
黄红 |
|
红 |
红白 |
红黄 |
红红 |
则P(两次都摸到红球)=.
5. (2011四川南充市,16,6分) 在一个不透明的口袋中装有4张相同的纸牌,它们分别标有数字1,2,3,4.随机地摸取出一张纸牌然后放回,在随机摸取出一张纸牌.
(1)计算两次摸取纸牌上数字之和为5的概率;
(2)甲、乙两个人进行游戏,如果两次摸出纸牌上数字之和为奇数,则甲胜;如果两次摸出纸牌上数字之和为偶数,则乙胜。这 是个公平的游戏吗?请说明理由.
[答案]解:用树状图法


 第一次: 1
2
3
4
第一次: 1
2
3
4
1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4
和 2 3 4 5 3 4 5 6 4 5 6 7 5 6 7 8
解法二:列表法
列表如下:
|
甲 乙 |
1 |
2 |
3 |
4 |
|
1 |
2 |
3 |
4 |
5 |
|
2 |
3 |
4 |
5 |
6 |
|
.3 |
4 |
5 |
6 |
7 |
|
4 |
5 |
6 |
7 |
8 |
由上表可以看出,摸取一张纸牌然后放回,再随机摸取出纸牌,可能结果有16种,它们出现的可能性相等.
(1)两次摸取纸牌上数字之和为5(记为事件A)有4个,P(A)=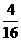 =
=
(2)这个游戏公平,理由如下:
两次摸出纸牌上数字之和为奇数(记为事件B)有8个,P(B)=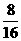 =
=
两次摸出纸牌上数字之和为偶数(记为事件C)有8个,P(C)=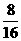 =
=
两次摸出纸牌上数字之和为奇数和为偶数的概率相同,所以这个游戏公平.
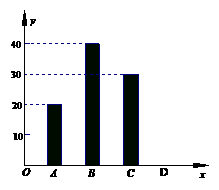
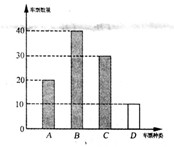
4. (2011山东烟台,23,12分)“五·一”假期,某公司组织部分员工分别到A、B、C、D四地旅游,公司按定额购买了前往各地的车票.下图是未制作完的车票种类和数量的条形统计图,根据统计图回答下列问题:
(1)若去D地的车票占全部车票的10%,请求出D地车票的数量,并补全统计图;
(2)若公司采用随机抽取的方式分发车票,每人抽取一张(所有车票的形状、大小、质地完全相同且充分洗匀),那么员工小胡抽到去A地的概率是多少?
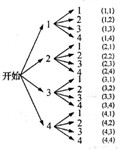
 (3)若有一张车票,小王、小李都想要,决定采取抛掷一枚各面分别标有1,2,3,4的正四面体骰子的方法来确定,具体规则是:“每人各抛掷一次,若小王掷得着地一面的数字比小李掷得着地一面的数字小,车票给小王,否则给小李”.试用“列表法或画树状图”的方法分析,这个规则对双方是否公平?
(3)若有一张车票,小王、小李都想要,决定采取抛掷一枚各面分别标有1,2,3,4的正四面体骰子的方法来确定,具体规则是:“每人各抛掷一次,若小王掷得着地一面的数字比小李掷得着地一面的数字小,车票给小王,否则给小李”.试用“列表法或画树状图”的方法分析,这个规则对双方是否公平?
[答案]解:(1)设D地车票有x张,则x=(x+20+40+30)×10%
 解得x=10.
解得x=10.
即D地车票有10张.
(2)小胡抽到去A地的概率为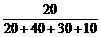 =
=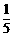 .
.
(3)以列表法说明
|
小李掷得数字 小王掷 得数字 |
1 |
2 |
3 |
4 |
|
1 |
(1,1) |
(1,2) |
(1,3) |
(1,4) |
|
2 |
(2,1) |
(2,2) |
(2,3) |
(2,4) |
|
3 |
(3,1) |
(3,2) |
(3,3) |
(3,4) |
|
4 |
(4,1) |
(4,2) |
(4,3) |
(4,4) |
或者画树状图法说明(如右上图)
由此可知,共有16种等可能结果.其中小王掷得数字比小李掷得数字小的有6种:(1,2),(1,3),(1,4),(2,3),(2,4),(3,4).
 ∴小王掷得数字比小李掷得数字小的概率为
∴小王掷得数字比小李掷得数字小的概率为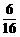 =
=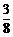 .
.
则小王掷得数字不小于小李掷得数字的概率为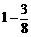 =
=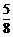 .
.
所以这个规则对双方不公平.
3. (2011山东威海,21,9分)甲、乙二人玩一个游戏,每人抛一个质地均匀的小立方体(每个面分别标有数字1、2、3、4、5、6),落定后,若两个小立方体朝上的数字之和为偶数,则甲胜;
若两个小立方体朝上的数字之和为奇数,则乙胜.你认为这个游戏公平吗?试说明理由.
[答案] 解:公平.
理由如下:每次游戏时,所有可能出现的结果如下:
 甲 甲乙 |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
(1,1) |
(1,2) |
(1,3) |
(1,4) |
(1,5) |
(1,6) |
|
2 |
(2,1) |
(2,2) |
(2,3) |
(2,4) |
(2,5) |
(2,6) |
|
3 |
(3,1) |
(3,2) |
(3,3) |
(3,4) |
(3,5) |
(3,6) |
|
4 |
(4,1) |
(4,2) |
(4,3) |
(4,4) |
(4,5) |
(4,6) |
|
5 |
(5,1) |
(5,2) |
(5,3) |
(5,4) |
(5,5) |
(5,6) |
|
6 |
(6,1) |
(6,2) |
(6,3) |
(6,4) |
(6,5) |
(6,6) |
总共有期36种结果,每种结果出现的可能性相同,其中两数字之和为偶数的有18种,两数字之和为奇数的有18种,每人获胜的概率均为 ,所以游戏是公平的.
,所以游戏是公平的.
2. (2011江苏扬州,22,8分)扬州市体育中考现场考试内容有三项:50米跑为必测项目;另在立定跳远、实心球(二选一)和坐位体前屈、1分钟跳绳(二选一)中选择两项。
(1)每位考生有 选择方案;
(2)用画树状图或列表的方法求小明与小刚选择同种方案的概率。(友情提醒:各种方案用A、B、C、…或①、②、③、…等符号来代表可简化解答过程)
[答案]解:(1)4;
(2)把4种中方案分别列为:
A:立定跳远、坐位体前屈;B:实心球、1分钟跳绳;
C:立定跳远、1分钟跳绳;D:实心球、坐位体前屈;
画树状图如下:
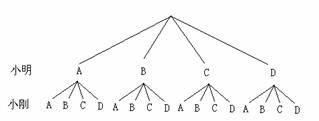
∴小明与小刚选择同种方案的概率=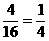
1. (2011安徽芜湖,22,10分)在复习《反比例函数》一课时,同桌的小明和小芳有一个问题观点不一致.小明认为如果两次分别从1-6六个整数中任取一个数,第一个数作为点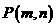 的横坐标,第二个数作为点
的横坐标,第二个数作为点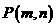 的纵坐标,则点
的纵坐标,则点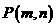 在反比例函数
在反比例函数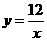 的图象上的概率一定大于在反比例函数
的图象上的概率一定大于在反比例函数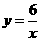 的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
的图象上的概率,而小芳却认为两者的概率相同.你赞成谁的观点?
(1)试用列表或画树状图的方法列举出所有点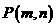 的情形;
的情形;
(2)分别求出点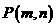 在两个反比例函数的图象上的概率,并说明谁的观点正确.
在两个反比例函数的图象上的概率,并说明谁的观点正确.
[答案]解: (1)列表如下: ………………………………………………………………6分

|
1 |
2 |
3 |
4 |
5 |
6 |
||||
|
1 |
(1,1 ) |
(1,2 ) |
(1,3 ) |
(1,4 ) |
(1,5 ) |
(1,6) |
||||
|
2 |
(2,1 ) |
(2,2 ) |
(2,3 ) |
(2,4 ) |
(2,5 ) |
(2,6) |
||||
|
3 |
(3,1 ) |
(3,2 ) |
(3,3 ) |
(3,4 ) |
(3,5 ) |
(3,6) |
||||
|
4 |
(4,1 ) |
(4,2 ) |
(4,3 ) |
(4,4 ) |
(4,5 ) |
(4,6) |
||||
|
5 |
(5,1) |
(5,2) |
(5,3 ) |
(5,4 ) |
(5,5 ) |
(5,6) |
||||
|
6 |
(6,1 ) |
(6,2) |
(6,3 ) |
(6,4 ) |
(6,5 ) |
(6,6) |
 画树状图如下: ………………………………………………………………6分
画树状图如下: ………………………………………………………………6分
(2)由树状图或表格可知,点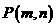 共有36种可能的结果,且每种结果出现的可能性相同,点(3,4),(4,3),(2,6),(6,2)在反比例函数
共有36种可能的结果,且每种结果出现的可能性相同,点(3,4),(4,3),(2,6),(6,2)在反比例函数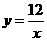 的图象上,……………7分
的图象上,……………7分
点 (2,3),(3,2),(1,6),(6,1)在反比例函数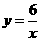 的图象上, …………………8分
的图象上, …………………8分
故点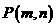 在反比例函数
在反比例函数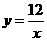 和
和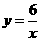 的图象上的概率相同,都是
的图象上的概率相同,都是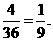 ………9分
………9分
所以小芳的观点正确. ………………………………………………………………10分
28.
27. (2011湖南湘潭市,14,3分) 端午节吃粽子是中华民族的习惯.今年农历五月初五早餐时,小明妈妈端上一盘粽子,其中有3个肉馅粽子和7个豆沙馅粽子,小明从中任意拿出一个,恰好拿到肉馅粽子的概率是_____.
[答案]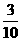
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com