
题目列表(包括答案和解析)
28. (2011江苏南通,25,9分)(本小题满分9分)
光明中学十分重视中学生的用眼卫生,并定期进行视力检测.某次检测设有A、B两处检测点,甲、乙、丙三名学生各自随机选择其中的一处检测视力.
(1) 求甲、乙、丙三名学生在同一处检测 视力的概率;
(2) 求甲、乙、丙三名学生中至少有两人在B处检测视力的概率.
[答案]∵甲、乙、丙的检测情况,有如下8种可能:
|
|
A |
B |
|
1 |
甲 |
乙丙 |
|
2 |
甲乙 |
丙 |
|
3 |
甲丙 |
乙 |
|
4 |
甲乙丙 |
|
|
5 |
乙 |
甲丙 |
|
6 |
乙丙 |
甲 |
|
7 |
丙 |
甲乙 |
|
8 |
|
甲乙丙 |
∴ (1)P(甲、乙、丙在同一处检测)=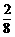 =
=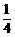 ;
;
(2)P(至少有两人在B处检测)=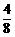 =
=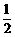 .
.
27. (2011江苏南京,23,7分)从3名男生和2名女生中随机抽取2014年南京青奥会志愿者.求下列事件的概率:
⑴抽取1名,恰好是女生;
⑵抽取2名,恰好是1名男生和1名女生.
[答案]解:⑴抽取1名,恰好是女生的概率是 .
.
⑵分别用男1、男2、男3、女1、女2表示这五位同学,从中任意抽取2名,所有可能出现的结果有:(男1,男2),(男1,男3),(男1,女1),(男1,女2),(男2,男3),(男2,女1),(男2,女2),(男3,女1),(男3,女2),(女1,女2),共10种,它们出现的可能性相同,所有结果中,满足抽取2名,恰好是1名男生和1名女生(记为事件A)的结果共6种,所以P(A)=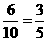 .
.
26. (2011江苏淮安,21,8分)如图,有牌面数字都是2,3,4的两组牌.从每组牌中各随机摸出一张,请用画树状图或列表的方法,求摸出的两张牌的牌面数字之和为6的概率.


[答案]解法一:画树状图如下:
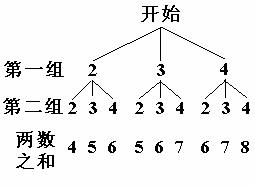
∵共有九种情况,数字之和为6的共有3种,
∴摸出的两张牌的牌面数字之和为6的概率为: .
.
解法二:列表如下:
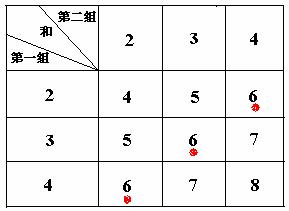
∵共有九种情况,数字之和为6的共有3种,
∴摸出的两张牌的牌面数字之和为6的概率为: .
.
25. (2011湖南怀化,19,10分)已知不等式组: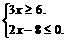
(1) 求满足此不等式组的所有整数解;
(2) 从此不等式的所有整数解中任取一个数,它是偶数的概率是多少?
[答案](1)解:解不等式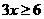 得,
得,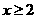 ;
;
解不等式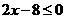 得,
得,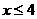 ;
;
所以原不等式组的解集为 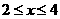
所以此不等式组的所有整数解为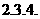
(2)从2,3,4中任意取出一个数,一共有3种情况,其中取出偶数的可能性有2,4两种,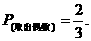
24. (2011江西南昌,18,6分)甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛,
⑴请用树状图法或列表法,求恰好选中甲、乙两位同学的概率;
⑵若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率。
[答案](1)方法一:
画树状图如下:

所有可能出现的情况有12种,其中甲乙两位同学组合的情况有两种,
所以P(甲乙)= =
= .
.
方法二:
列表法如下:
|
|
甲 |
乙 |
丙 |
丁 |
|
甲 |
|
乙甲 |
丙甲 |
丁甲 |
|
乙 |
甲乙 |
|
丙乙 |
丁乙 |
|
丙 |
甲丙 |
乙丙 |
|
乙丙 |
|
丁 |
甲丙 |
乙丁 |
丙丁 |
|
所有可能出现的情况有12种,其中甲乙两位同学组合的情况有两种,
所以P(甲乙)= =
= .
.
(2)若已确定甲打第一场,再从其余三位同学中随机选取一位,共有3种情况选中乙的情况有一种,所以P(恰好选中乙同学)= .
.
23. (2011重庆綦江,22,10分)我县实施新课程改革后,学生的自主学习、合作交流能力有很大提高,张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
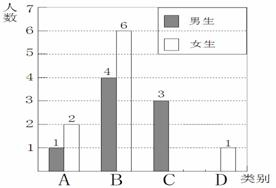
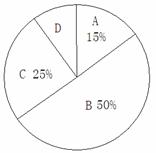
(1)本次调查中,张老师一共调查了 名同学,其中C类女生有 名,
D类男生有 名;
(2)将上面的条形统计图补充完整;
(3)为了共同进步,张老师想从被调查的A类和D类学生中分别选取一位同学进行
“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位
男同学和一位女同学的概率.
[答案]:(1)20,(2分) 2 ,(1分) 1(1分);
(2) 如图(2分,各1分)
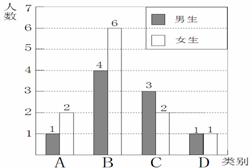
(3)选取情况如下:
(列表或树形图正确3分、计算概率1分)
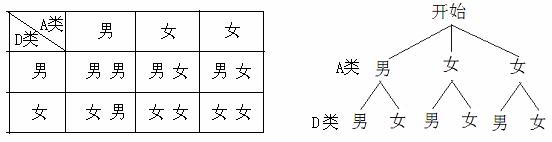
∴所选两位同学恰好是一位男同学和一位女同学的概率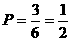
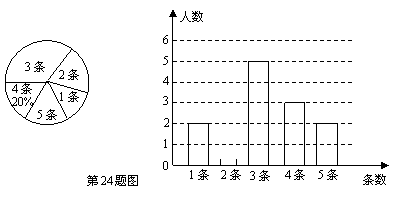
22. ( 2011重庆江津, 24,10分)在“传箴言”活动中,某党支部对全体党员在一个月内所发箴言条数情况进行了统计,并制成了如下两幅不完整的统计图.
(1)求该支部党员在这一个月内所发箴言的平均条数是多少?并将该条形统计图补充完整;
 (2)如果发了三条箴言的党员中有两位男党员,发了四条箴言的党员有两位女党员,在发了三条箴言和四条箴言的党员中分别选出一位参加区委组织的“传箴言”活动总结会,请你用列表或树状图的方法,求出所选两位党员恰好是一男一女的概率.
(2)如果发了三条箴言的党员中有两位男党员,发了四条箴言的党员有两位女党员,在发了三条箴言和四条箴言的党员中分别选出一位参加区委组织的“传箴言”活动总结会,请你用列表或树状图的方法,求出所选两位党员恰好是一男一女的概率.
[答案](1)由图形可知,总人数为:3÷20﹪=15(人)
发两条的人数:15-2-5-3-2=3(人)·
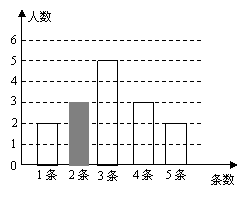 图形如图
图形如图
平均条数=(1×2+2×3+3×5+4×3+5×2)÷15=3(条)·
(2)树状图


|
|
男 |
男 |
女 |
女 |
女 |
|
男 |
(男,男) |
(男,男) |
(男,女) |
(男,女) |
(男,女) |
|
女 |
(女,男) |
(女,男) |
(女,女) |
(女,女) |
(女,女) |
|
女 |
(女,男) |
(女,男) |
(女,女) |
(女,女) |
(女,女) |
∴P(一男一女)=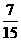 ·
·
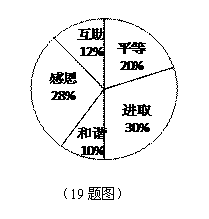
21. (2011四川宜宾,19,8分)某校开展了以“人生观、价值观”为主题的班队活动,活动结束后,初三(2)班数学兴趣小组提出了5个主要观点并在本班50名学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图.
(1)该班学生选择“和谐”观点的有___________人,在扇形统计图中,“和谐”观点所在扇形区域的圆心角是____________度.
(2)如果该校有1500名初三学生,利用样本估计选择“感恩”观点的初三学生约有___________人.
(3)如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查,求恰好选到“和谐”和“感恩”观点的概率(用树状图或列表法分析解答).

[答案]⑴5,36;
⑵420;
⑶以下两种方式任选一种
(用树状图)设平等、进取、和谐、感恩、互助的序号依次是①②③④⑤
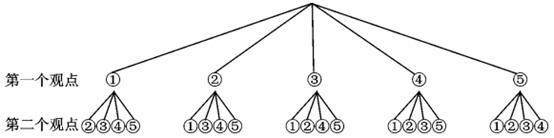
∴恰好选到“和谐”和“感恩”观点的概率是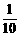 .
.
(用列表法)
|
|
平等 |
进取 |
和谐 |
感恩 |
互助 |
|
平等 |
|
平等、进取 |
平等、和谐 |
平等、感恩 |
平等、互助 |
|
进取 |
进取、平等 |
|
进取、和谐 |
进取、感恩 |
进取、互助 |
|
和谐 |
和谐、平等 |
和谐、进取 |
|
和谐、感恩 |
和谐、互助 |
|
感恩 |
感恩、平等 |
感恩、进取 |
感恩、和谐 |
|
感恩、互助 |
|
互助 |
互助、平等 |
互助、取 |
互助、和谐 |
互助、感恩 |
|
∴恰好选到“和谐”和“感恩”观点的概率是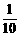 .
.
20.(2011四川内江,19,9分)小英和小明姐弟二人准备一起去观看端午节龙舟赛,但因家中临时有事,必须留下一人在家,于是姐弟二人采用游戏的方式来确定谁去看龙舟赛。游戏规则是:在不透明的口袋中分别放入2个白色和1个黄色的乒乓球,它们除颜色外其余都相同。游戏时先由小英从口袋中任意摸出1个乒乓球记下颜色后放回并摇匀,再由小明从口袋中摸出1个乒乓球,记下颜色。如果姐弟二人摸到的乒乓球颜色相同,则小英赢,否则小明赢。
(1)请用树状图或列表的方法表示游戏中所有可能出现的结果。
(2)这个游戏规则对游戏双方公平吗?请说明理由。
[答案](1)白色 白白 白白 白黄
白色 白白 白白 白黄
黄色 黄白 黄白 黄黄
 白色 白色 黄色
白色 白色 黄色
共有9种结果
(2)双方不公平
因小英胜的概率为 ,小明胜的概率为
,小明胜的概率为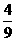 ,所以不公平。
,所以不公平。
19. (2011四川成都,18,8分)某市今年的信息技术结业考试,采用学生抽签的方式决定自己的考试内容。规定:每位考生先在三个笔试题(题签分别用代码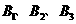 表示)中抽取一个,再在三个上机题(题签分别用代码
表示)中抽取一个,再在三个上机题(题签分别用代码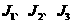 表示)中抽取一个进行考试.小亮在看不到题签的情况下,分别从笔试题和上机题中随机地各抽取一个题签.
表示)中抽取一个进行考试.小亮在看不到题签的情况下,分别从笔试题和上机题中随机地各抽取一个题签.
(1)用树状图或列表法表示出所有可能的结构;
(2)求小亮抽到的笔试题和上机题的题签代码的下标(例如“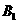 ”的下表为“1”)均为奇数的概率.
”的下表为“1”)均为奇数的概率.
[答案]解:(1)方法一:画树状图
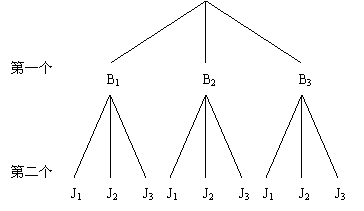

方法二:列表如下
|
第一个 第二个 |
B1 |
B2 |
B3 |
|
J1 |
(B1 ,J1 ) |
(B2,J1 ) |
(B3,J1 ) |
|
J2 |
(B1 ,J2 ) |
(B2,J2 ) |
(B3,J2 ) |
|
J3 |
(B1 ,J3 ) |
(B2,J3 ) |
(B3,J3 ) |
(2)根据树状图或列表法得出所有可能数为9,两次抽取题签代码的下标为奇数是(B1 ,J1 ),(B3,J1 ),(B1 ,J3 ),(B3,J3 ),共4种,所以求小亮抽到的笔试题和上机题的题签代码的下标均为奇数的概率为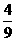 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com