
题目列表(包括答案和解析)
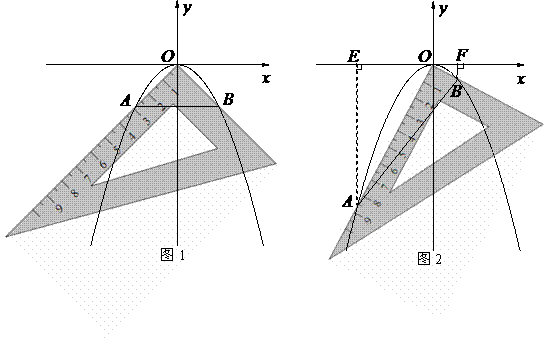
24.(株洲市2011年)(本题满分10分)孔明是一个喜欢探究钻研的同学,他在和同学们一起研究某条抛物线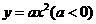 的性质时,将一把直角三角板的直角顶点置于平面直角坐标系的原点
的性质时,将一把直角三角板的直角顶点置于平面直角坐标系的原点 ,两直角边与该抛物线交于
,两直角边与该抛物线交于 、
、 两点,请解答以下问题:
两点,请解答以下问题:
(1)若测得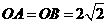 (如图1),求
(如图1),求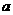 的值;
的值;
(2)对同一条抛物线,孔明将三角板绕点 旋转到如图2所示位置时,过
旋转到如图2所示位置时,过 作
作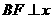 轴于点
轴于点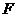 ,测得
,测得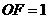 ,写出此时点
,写出此时点 的坐标,并求点
的坐标,并求点 的横坐标;
的横坐标;
(3)对该抛物线,孔明将三角板绕点 旋转任意角度时惊奇地发现,交点
旋转任意角度时惊奇地发现,交点 、
、 的连线段总经过一个固定的点,试说明理由并求出该点的坐标.
的连线段总经过一个固定的点,试说明理由并求出该点的坐标.
23、解:(1)、
 ∵y轴和直线l都是⊙C的切线
∵y轴和直线l都是⊙C的切线
∴OA⊥AD BD⊥AD
又∵ OA⊥OB
∴∠AOB=∠OAD=∠ADB=90°
∴四边形OADB是矩形
∵⊙C的半径为2
∴AD=OB=4
∵点P在直线l上
∴点P的坐标为(4,p)
又∵点P也在直线AP上
∴p=4k+3
(2)连接DN
∵AD是⊙C的直径 ∴ ∠AND=90°
∵ ∠AND=90°-∠DAN,∠ABD=90°-∠DAN
∴∠AND=∠ABD
又∵∠ADN=∠AMN ∴∠ABD=∠AMN …………4分
∵∠MAN=∠BAP …………5分
∴△AMN∽△ABP …………6分
(3)存在。 …………7分
理由:把x=0代入y=kx+3得y=3,即OA=BD=3
AB=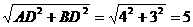
∵ S△ABD=
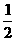 AB·DN=
AB·DN=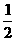 AD·DB
AD·DB
∴DN=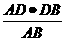 =
=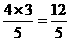
∴AN2=AD2-DN2=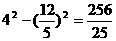
∵△AMN∽△ABP
∴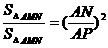 即
即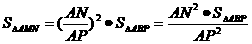 ……8分
……8分
当点P在B点上方时,
∵AP2=AD2+PD2 = AD2+(PB-BD)2 =42+(4k+3-3)2 =16(k2+1)
或AP2=AD2+PD2 = AD2+(BD-PB)2 =42+(3-4k-3)2 =16(k2+1)
S△ABP=
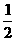 PB·AD=
PB·AD=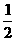 (4k+3)×4=2(4k+3)
(4k+3)×4=2(4k+3)
∴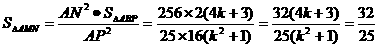
整理得k2-4k-2=0 解得k1 =2+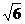 k2=2-
k2=2-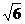 …………9分
…………9分
当点P在B 点下方时,
∵AP2=AD2+PD2 =42+(3-4k-3)2 =16(k2+1)
S△ABP=
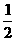 PB·AD=
PB·AD=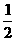 [-(4k+3)]×4=-2(4k+3)
[-(4k+3)]×4=-2(4k+3)
∴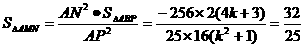
化简,得k2+1=-(4k+3) 解得k=-2
综合以上所得,当k=2±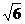 或k=-2时,△AMN的面积等于
或k=-2时,△AMN的面积等于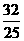 …10分
…10分
28. 解:(1)根据题意,得,解得 ,∴A(3,4) .
解:(1)根据题意,得,解得 ,∴A(3,4) .
令y=-x+7=0,得x=7.∴B(7,0).
(2)①当P在OC上运动时,0≤t<4.
由S△APR=S梯形COBA-S△ACP-S△POR-S△ARB=8,得
(3+7)×4-×3×(4-t)- t(7-t)- t×4=8
整理,得t2-8t+12=0, 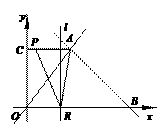 解之得t1=2,t2=6(舍)
解之得t1=2,t2=6(舍)
当P在CA上运动,4≤t<7.
由S△APR= ×(7-t) ×4=8,得t=3(舍)
∴当t=2时,以A、P、R为顶点的三角形的面积为8.
②当P在OC上运动时,0≤t<4.
∴AP=,AQ=t,PQ=7-t
当AP =AQ时, (4-t)2+32=2(4-t)2,
整理得,t2-8t+7=0. ∴t=1, t=7(舍)
当AP=PQ时,(4-t)2+32=(7-t)2,
 整理得,6t=24. ∴t=4(舍去)
整理得,6t=24. ∴t=4(舍去)
当AQ=PQ时,2(4-t)2=(7-t)2
整理得,t2-2t-17=0 ∴t=1±3 (舍)
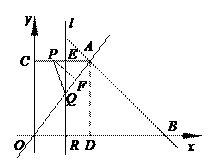
当P在CA上运动时,4≤t<7. 过A作AD⊥OB于D,则AD=BD=4.
设直线l交AC于E,则QE⊥AC,AE=RD=t-4,AP=7-t.
由cos∠OAC= = ,得AQ = (t-4).
 当AP=AQ时,7-t = (t-4),解得t = .
当AP=AQ时,7-t = (t-4),解得t = .
当AQ=PQ时,AE=PE,即AE= AP
得t-4= (7-t),解得t =5.
当AP=PQ时,过P作PF⊥AQ于F
AF= AQ = ×(t-4).
在Rt△APF中,由cos∠PAF= = ,得AF= AP
即 ×(t-4)= ×(7-t),解得t= .
∴综上所述,t=1或 或5或 时,△APQ是等腰三角形.
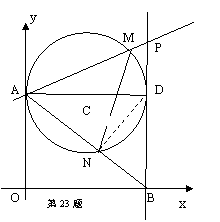
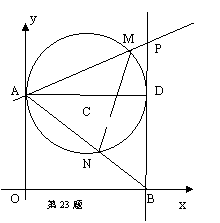
(2011·济宁)如图,第一象限内半径为2的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+3。
(1) 设点P的纵坐标为p,写出p随变化的函数关系式。
(2)设⊙C与PA交于点M,与AB交于点N,则不论动点P处于直线l上(除点B以外)的什么位置时,都有△AMN∽△ABP。请你对于点P处于图中位置时的两三角形相似给予证明;
 (3)是否存在使△AMN的面积等于
(3)是否存在使△AMN的面积等于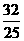 的k值?若存在,请求出符合的k值;若不存在,请说明理由。
的k值?若存在,请求出符合的k值;若不存在,请说明理由。
27.解:情境观察
AD(或A′D),90
问题探究
结论:EP=FQ.
证明:∵△ABE是等腰三角形,∴AB=AE,∠BAE=90°.
∴∠BAG+∠EAP=90°.∵AG⊥BC,∴∠BAG+∠ABG=90°,∴∠ABG=∠EAP.
∵EP⊥AG,∴∠AGB=∠EPA=90°,∴Rt△ABG≌Rt△EAP. ∴AG=EP.
同理AG=FQ. ∴EP=FQ.
拓展延伸
 结论: HE=HF.
结论: HE=HF.
理由:过点E作EP⊥GA,FQ⊥GA,垂足分别为P、Q.
∵四边形ABME是矩形,∴∠BAE=90°,
∴∠BAG+∠EAP=90°.AG⊥BC,∴∠BAG+∠ABG=90°,
∴∠ABG=∠EAP.
∵∠AGB=∠EPA=90°,∴△ABG∽△EAP,∴ = .
同理△ACG∽△FAQ,∴ = .
∵AB= k AE,AC= k AF,∴ = = k,∴ = . ∴EP=FQ.
∵∠EHP=∠FHQ,∴Rt△EPH≌Rt△FQH. ∴HE=HF
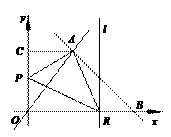
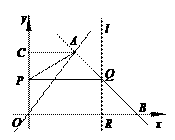
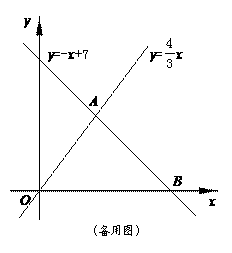
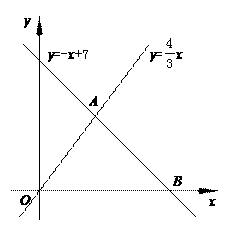
(盐城市二○一一年)28.(本题满分12分)如图,已知一次函数y = - x +7与正比例函数y = x的图象交于点A,且与x轴交于点B.
(1)求点A和点B的坐标;
(2)过点A作AC⊥y轴于点C,过点B作直线l∥y轴.动点P从点O出发,以每秒1个单位长的速度,沿O-C-A的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒.
①当t为何值时,以A、P、R为顶点的三角形的面积为8?
②是否存在以A、P、Q为顶点的三角形是等腰三角形?若存在,求t的值;若不存在,请说明理由.
28.(1)∵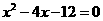 ,∴
,∴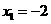 ,
,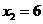 。
。
∴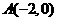 ,
,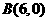 。····················1分
。····················1分
又∵抛物线过点 、
、 、
、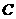 ,
,
故设抛物线的解析式为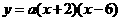 ,
,
将点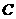 的坐标代入,求得
的坐标代入,求得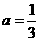 。
。
∴抛物线的解析式为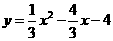 。········3分
。········3分
(2)设点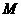 的坐标为(
的坐标为( ,0),过点
,0),过点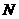 作
作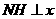 轴于点
轴于点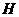 (如图(1))。
(如图(1))。
∵点 的坐标为(
的坐标为(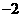 ,0),点
,0),点 的坐标为(6,0),
的坐标为(6,0),
∴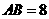 ,
,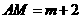 。···························4分
。···························4分
∵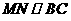 ,∴
,∴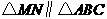 。
。
∴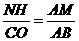 ,∴
,∴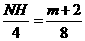 ,∴
,∴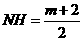 。·················5分
。·················5分
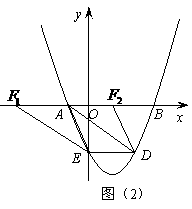 ∴
∴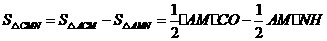
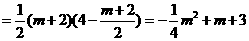 ······6分
······6分
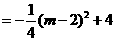 。
。
∴当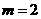 时,
时,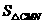 有最大值4。
有最大值4。
此时,点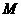 的坐标为(2,0)。··············7分
的坐标为(2,0)。··············7分
(3)∵点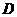 (4,
(4,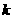 )在抛物线
)在抛物线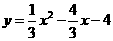 上,
上,
 ∴当
∴当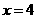 时,
时,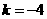 ,
,
∴点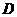 的坐标是(4,
的坐标是(4,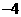 )。
)。
如图(2),当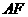 为平行四边形的边时,
为平行四边形的边时,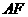


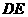 ,
,
∵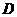 (4,
(4,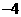 ),∴
),∴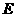 (0,
(0,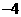 ),
),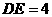 。
。
∴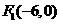 ,
,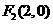 。 ··········9分
。 ··········9分
①
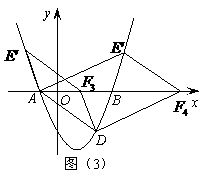
如图(3),当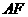 为平行四边形的对角线时,
为平行四边形的对角线时,
设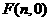 ,则平行四边形的对称中心为
,则平行四边形的对称中心为
(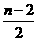 ,0)。·················10分
,0)。·················10分
∴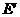 的坐标为(
的坐标为(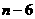 ,4)。
,4)。
把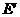 (
(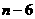 ,4)代入
,4)代入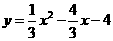 ,得
,得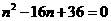 。
。
解得 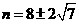 。
。
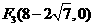 ,
,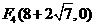 。····
。····
(盐城市二○一一年)27.(本题满分12分)
情境观察
将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.
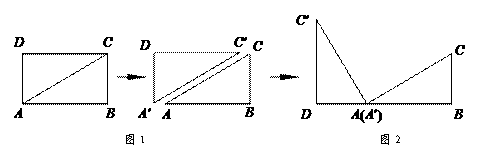 观察图2可知:与BC相等的线段是 ▲
,∠CAC′= ▲
°.
观察图2可知:与BC相等的线段是 ▲
,∠CAC′= ▲
°.
问题探究
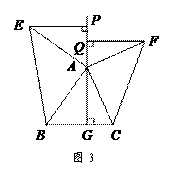 如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q. 试探究EP与FQ之间的数量关系,并证明你的结论.
如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q. 试探究EP与FQ之间的数量关系,并证明你的结论.
拓展延伸
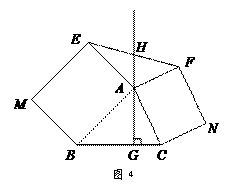 如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H. 若AB= k AE,AC= k AF,试探究HE与HF之间的数量关系,并说明理由.
如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H. 若AB= k AE,AC= k AF,试探究HE与HF之间的数量关系,并说明理由.
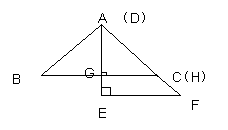
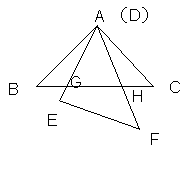
21.(2011年广东省)如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=AC=EF=9,∠BAC=∠DEF=90º,固定△ABC,将△DEF绕点A顺时针旋转,当DF边与AB边重合时,旋转中止.现不考虑旋转开始和结束时重合的情况,设DE,DF(或它们的延长线)分别交BC(或它的延长线) 于G,H点,如图(2)
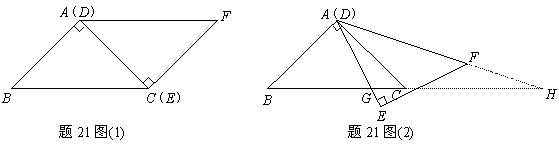
(1)问:始终与△AGC相似的三角形有 及 ;
(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据图(2)的情形说明理由)
(3)问:当x为何值时,△AGH是等腰三角形.
(1)、△HAB △HGA;
(2)、由△AGC∽△HAB,得AC/HB=GC/AB,即9/y=x/9,故y=81/x
(0<x<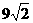 )
)
(3)因为:∠GAH= 45°
①当∠GAH= 45°是等腰三角形.的底角时,如图(1):可知CG=x=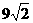 /2
/2
②当∠GAH= 45°是等腰三角形.的顶角时, 如图(2):由△HGA∽△HAB
知:HB= AB=9,也可知BG=HC,可得:CG=x=18-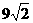


图(1) 图(2)
(2011年凉山州)如图,抛物线与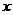 轴交于
轴交于 (
(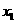 ,0)、
,0)、 (
(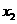 ,0)两点,且
,0)两点,且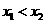 ,与
,与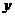 轴交于点
轴交于点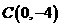 ,其中
,其中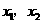 是方程
是方程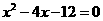 的两个根。
的两个根。
(1)求抛物线的解析式;
(2)点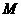 是线段
是线段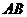 上的一个动点,过点
上的一个动点,过点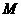 作
作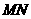 ∥
∥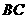 ,交
,交 于点
于点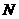 ,连接
,连接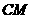 ,当
,当 的面积最大时,求点
的面积最大时,求点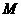 的坐标;
的坐标;
(3)点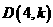 在(1)中抛物线上,点
在(1)中抛物线上,点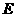 为抛物线上一动点,在
为抛物线上一动点,在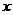 轴上是否存在点
轴上是否存在点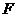 ,使以
,使以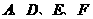 为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点
为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点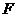 的坐标,若不存在,请说明理由。
的坐标,若不存在,请说明理由。
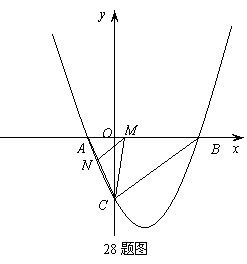
10.(2011年广东省)如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE,它的面积为1;取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图(2)中阴影部分;取△A1B1C1和△D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2,如图(3)中阴影部分;如此下去…,则正六角星形A4F4B4D4C4E4的面积为_________________.

答案: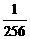
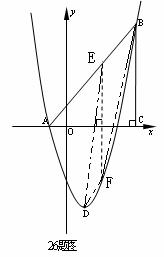
26. 解:(1)由已知得:A(-1,0) B(4,5)------------1分
 ∵二次函数
∵二次函数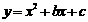 的图像经过点A(-1,0)B(4,5)
的图像经过点A(-1,0)B(4,5)
∴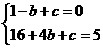 ------------2分
------------2分
解得:b=-2 c=-3 ------------3分
(2如26题图:∵直线AB经过点A(-1,0) B(4,5)
∴直线AB的解析式为:y=x+1
∵二次函数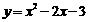
∴设点E(t, t+1),则F(t,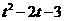 ) ------------4分
) ------------4分
∴EF= 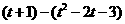 ------------5分
------------5分
=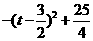
 ∴当
∴当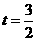 时,EF的最大值=
时,EF的最大值=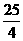
∴点E的坐标为(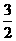 ,
,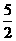 ) ------------------------6分
) ------------------------6分
(3)①如26题图:顺次连接点E、B、F、D得四边形EBFD.
可求出点F的坐标(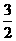 ,
,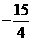 ),点D的坐标为(1,-4)
),点D的坐标为(1,-4)
S = S
= S + S
+ S
=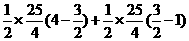
|
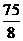 -----------------------------------9分
-----------------------------------9分
②如26题备用图:ⅰ)过点E作a⊥EF交抛物线于点P,设点P(m,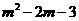 )
)
则有: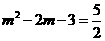 解得:
解得: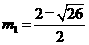 ,
,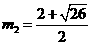
∴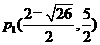 ,
, 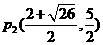
ⅱ)过点F作b⊥EF交抛物线于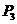 ,设
,设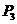 (n,
(n,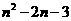 )
)
则有: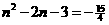 解得:
解得: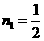 ,
,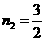 (与点F重合,舍去)∴
(与点F重合,舍去)∴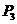
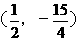
综上所述:所有点P的坐标: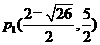 ,
,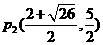
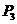 (
(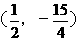 . 能使△EFP组成以EF为直角边的直角三角形.------------------------------------12分
. 能使△EFP组成以EF为直角边的直角三角形.------------------------------------12分
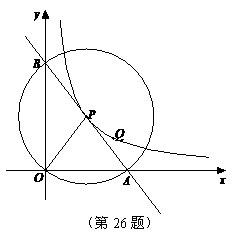
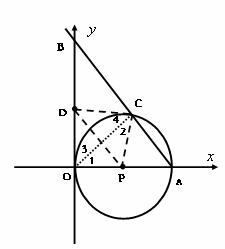
(江苏省宿迁市2011年)26.(本题满分10分)如图,在平面直角坐标系中,O为坐标原点,P是反比例函数y=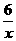 (x>0)图象上的任意一点,以P为圆心,PO为半径的圆与x、y轴分别交于点A、B.
(x>0)图象上的任意一点,以P为圆心,PO为半径的圆与x、y轴分别交于点A、B.
(1)判断P是否在线段AB上,并说明理由;
(2)求△AOB的面积;
 (3)Q是反比例函数y=
(3)Q是反比例函数y=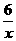 (x>0)图象上异于点P的另一点,请以Q为圆心,QO
(x>0)图象上异于点P的另一点,请以Q为圆心,QO
半径画圆与x、y轴分别交于点M、N,连接AN、MB.求证:AN∥MB.
解:(1)点P在线段AB上,理由如下:
∵点O在⊙P上,且∠AOB=90°
∴AB是⊙P的直径
∴点P在线段AB上.
(2)过点P作PP1⊥x轴,PP2⊥y轴,由题意可知PP1、PP2
是△AOB的中位线,故S△AOB=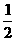 OA×OB=
OA×OB=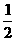 ×2 PP1×PP2
×2 PP1×PP2
∵P是反比例函数y=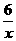 (x>0)图象上的任意一点
(x>0)图象上的任意一点
∴S△AOB=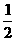 OA×OB=
OA×OB=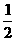 ×2 PP1×2PP2=2 PP1×PP2=12.
×2 PP1×2PP2=2 PP1×PP2=12.
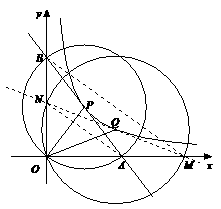 (3)如图,连接MN,则MN过点Q,且S△MON=S△AOB=12.
(3)如图,连接MN,则MN过点Q,且S△MON=S△AOB=12.
∴OA·OB=OM·ON
∴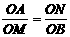
∵∠AON=∠MOB
∴△AON∽△MOB
∴∠OAN=∠OMB
∴AN∥MB.
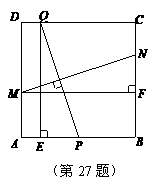
(江苏省宿迁市2011年)27.(本题满分12分)如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.
(1)当t≠1时,求证:△PEQ≌△NFM;
(2)顺次连接P、M、Q、N,设四边形PMQN的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值.
 解:(1)∵四边形ABCD是正方形
解:(1)∵四边形ABCD是正方形
∴∠A=∠B=∠D=90°,AD=AB
∵QE⊥AB,MF⊥BC
∴∠AEQ=∠MFB=90°
∴四边形ABFM、AEQD都是矩形
∴MF=AB,QE=AD,MF⊥QE
又∵PQ⊥MN
∴∠EQP=∠FMN
又∵∠QEP=∠MFN=90°
∴△PEQ≌△NFM.
(2)∵点P是边AB的中点,AB=2,DQ=AE=t
∴PA=1,PE=1-t,QE=2
由勾股定理,得PQ=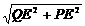 =
=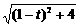
∵△PEQ≌△NFM
∴MN=PQ=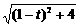
又∵PQ⊥MN
∴S=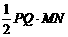 =
=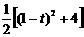 =
=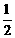 t2-t+
t2-t+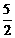
∵0≤t≤2
∴当t=1时,S最小值=2.
综上:S=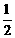 t2-t+
t2-t+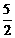 ,S的最小值为2.
,S的最小值为2.
(江苏省宿迁市2011年)28.(本题满分12分)如图,在Rt△ABC中,∠B=90°,AB=1,BC=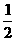 ,以点C为圆心,CB为半径的弧交CA于点D;以点A为圆心,AD为半径的弧交AB于点E.
,以点C为圆心,CB为半径的弧交CA于点D;以点A为圆心,AD为半径的弧交AB于点E.
(1)求AE的长度;
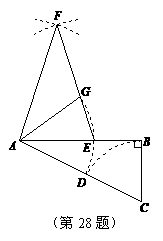 (2)分别以点A、E为圆心,AB长为半径画弧,两弧交于点F(F与C在AB两侧),连接AF、EF,设EF交弧DE所在的圆于点G,连接AG,试猜想∠EAG的大小,并说明理由.
(2)分别以点A、E为圆心,AB长为半径画弧,两弧交于点F(F与C在AB两侧),连接AF、EF,设EF交弧DE所在的圆于点G,连接AG,试猜想∠EAG的大小,并说明理由.
解:(1)在Rt△ABC中,由AB=1,BC=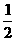 得 AC=
得 AC=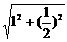 =
=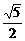
∵BC=CD,AE=AD
∴AE=AC-AD=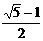 .
.
(2)∠EAG=36°,理由如下:
∵FA=FE=AB=1,AE=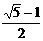
∴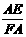 =
=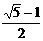
∴△FAE是黄金三角形
∴∠F=36°,∠AEF=72°
∵AE=AG,FA=FE
∴∠FAE=∠FEA=∠AGE
∴△AEG∽△FEA
∴∠EAG=∠F=36°.
25、解:(1)根据已知条件可设抛物线的解析式为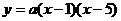 ,············1分
,············1分
把点A(0,4)代入上式得: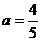 ,
,
∴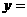
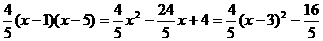 ,···········2分
,···········2分
∴抛物线的对称轴是: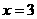 .······································3分
.······································3分
(2)由已知,可求得P(6,4). ···································5分
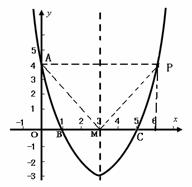 提示:由题意可知以A、O、M、P为顶点的四边形有两条边AO=4、OM=3,又知点P的坐标中
提示:由题意可知以A、O、M、P为顶点的四边形有两条边AO=4、OM=3,又知点P的坐标中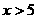 ,所以,MP>2,AP>2;因此以1、2、3、4为边或以2、3、4、5为边都不符合题意,所以四条边的长只能是3、4、5、6的一种情况,在Rt△AOM中,
,所以,MP>2,AP>2;因此以1、2、3、4为边或以2、3、4、5为边都不符合题意,所以四条边的长只能是3、4、5、6的一种情况,在Rt△AOM中,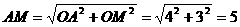 ,因为抛物线对称轴过点M,所以在抛物线
,因为抛物线对称轴过点M,所以在抛物线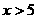 的图象上有关于点A的对称点与M的距离为5,即PM=5,此时点P横坐标为6,即AP=6;故以A、O、M、P为顶点的四边形的四条边长度分别是四个连续的正整数3、4、5、6成立,
的图象上有关于点A的对称点与M的距离为5,即PM=5,此时点P横坐标为6,即AP=6;故以A、O、M、P为顶点的四边形的四条边长度分别是四个连续的正整数3、4、5、6成立,
即P(6,4).···································5分
(注:如果考生直接写出答案P(6,4),给满分2分,但考生答案错误,解答过程分析合理可酌情给1分)
⑶法一:在直线AC的下方的抛物线上存在点N,使△NAC面积最大.
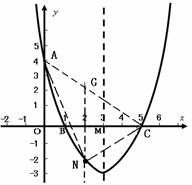 设N点的横坐标为
设N点的横坐标为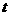 ,此时点N
,此时点N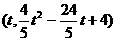 (
(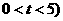 ,过点N作NG∥
,过点N作NG∥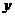 轴交AC于G;由点A(0,4)和点C(5,0)可求出直线AC的解析式为:
轴交AC于G;由点A(0,4)和点C(5,0)可求出直线AC的解析式为: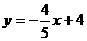 ;把
;把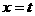 代入得:
代入得: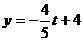 ,则G
,则G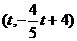 ,
,
此时:NG=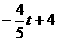 -(
-(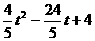 ),
),
=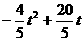 . ······································7分
. ······································7分
∴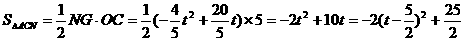
∴当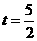 时,△CAN面积的最大值为
时,△CAN面积的最大值为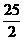 ,
,
由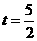 ,得:
,得: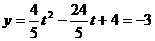 ,∴N(
,∴N(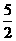 , -3). ········ 8分
, -3). ········ 8分
法二:提示:过点N作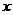 轴的平行线交
轴的平行线交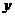 轴于点E,作CF⊥EN于点F,则
轴于点E,作CF⊥EN于点F,则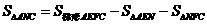
(再设出点N的坐标,同样可求,余下过程略)
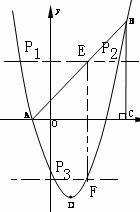
(重庆市潼南县2011年)26.(12分)如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90,AC=BC,OA=1,
OC=4,抛物线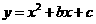 经过A,B两点,抛物线的顶点为D.
经过A,B两点,抛物线的顶点为D.
(1)求b,c的值;
(2)点E是直角三角形ABC斜边AB上一动点(点A、B除外),过点E作x轴的垂线
交抛物线于点F,当线段EF的长度最大时,求点E的坐标;
(3)在(2)的条件下:①求以点E、B、F、D为顶点的四边形的面积;②在抛物线上
是否存在一点P,使△EFP是以EF为直角边的直角三角形? 若存在,求出所有点P的坐标;若不存在,说明理由.
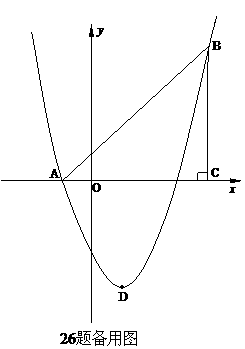
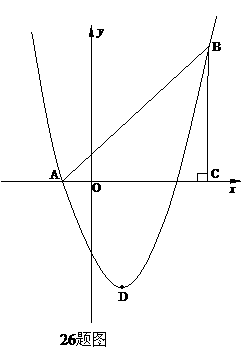
24、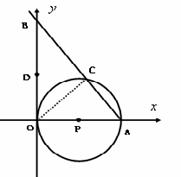 解:(1)解法一:连接OC,∵OA是⊙P的直径,∴OC⊥AB,
解:(1)解法一:连接OC,∵OA是⊙P的直径,∴OC⊥AB,
在Rt△AOC中,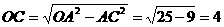 ,1分
,1分
在 Rt△AOC和Rt△ABO中,∵∠CAO=∠OAB
∴Rt△AOC∽Rt△ABO,····························2分
∴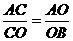 ,即
,即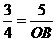 , ····················3分
, ····················3分
∴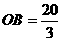 , ∴
, ∴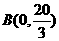 ····················4分
····················4分
解法二:连接OC,因为OA是⊙P的直径, ∴∠ACO=90°
在Rt△AOC中,AO=5,AC=3,∴OC=4, ············1分
过C作CE⊥OA于点E,则: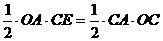 ,
,
即: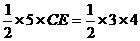 ,∴
,∴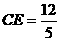 ,·························2分
,·························2分
∴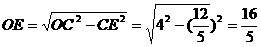 ∴
∴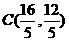 ,·········3分
,·········3分
 设经过A、C两点的直线解析式为:
设经过A、C两点的直线解析式为: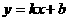 .
.
把点A(5,0)、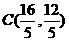 代入上式得:
代入上式得:
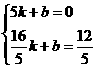 , 解得:
, 解得: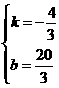 ,
,
∴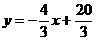 , ∴点
, ∴点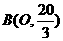 .·4分
.·4分
(2)点O、P、C、D四点在同一个圆上,理由如下:
连接CP、CD、DP,∵OC⊥AB,D为OB上的中点,
∴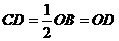 ,
,
∴∠3=∠4,又∵OP=CP,∴∠1=∠2,∴∠1+∠3=∠2+∠4=90°,
∴PC ⊥CD,又∵DO⊥OP,∴Rt△PDO和Rt△PDC是同以PD为斜边的直角三角形,∴PD上的中点到点O、P、C、D四点的距离相等,
∴点O、P、C、D在以DP为直径的同一个圆上; ·················6分
由上可知,经过点O、P、C、D的圆心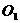 是DP的中点,圆心
是DP的中点,圆心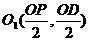 ,
,
由(1)知:Rt△AOC∽Rt△ABO,∴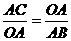 ,求得:AB=
,求得:AB=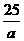 ,在Rt△ABO中,
,在Rt△ABO中,
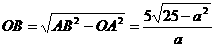 ,OD=
,OD=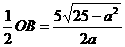 ,
,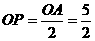
∴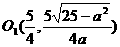 ,点
,点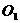 在函数
在函数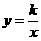 的图象上,
的图象上,
∴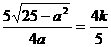 , ∴
, ∴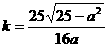
 . ················8分
. ················8分
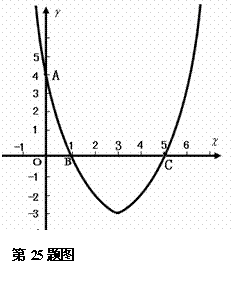
(2011年广东茂名市)如图,在平面直角坐标系 中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴
中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴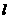 与
与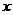 轴相交于点M.
轴相交于点M.
(1)求抛物线的解析式和对称轴; (3分)
(2)设点P为抛物线(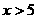 )上的一点,若以A、O、M、P为顶点的四边形四条边的长度为四个连续的正整数,请你直接写出点P的坐标;
(2分)
)上的一点,若以A、O、M、P为顶点的四边形四条边的长度为四个连续的正整数,请你直接写出点P的坐标;
(2分)
(3)连接AC.探索:在直线AC下方的抛物线上是否存在一点N,使△NAC的面积最大?若存在,请你求出点N的坐标;若不存在,请你说明理由. (3分)
 解:
解:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com