
题目列表(包括答案和解析)
38. (2011广东肇庆,18,6分)如图是一个转盘,转盘分成8个相同的扇形,颜色分为红、绿、黄三种.指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形).求下列事件的概率:
(1)指针指向红色;
(2)指针指向黄色或绿色.


[答案]解:按颜色把8个扇形分为红1、红2、绿1、绿2、绿3、黄1、黄2、黄3,所有可能结果的总数为8.
(1)指针指向红色的结果有2个, ∴ P(指针指向红色)=
(2)指针指向黄色或绿色的结果有3+3 = 6个 ,
∴
P(指针指向黄色或绿色)
37. (2011广东茂名,19,7分)从甲学校到乙学校有 、
、 、
、 三条线路,从乙学校到丙学校有
三条线路,从乙学校到丙学校有 、
、 二条线路.
二条线路.
(1)利用树状图或列表的方法表示从甲学校到丙学校的线路中所有可能出现的结果;(4分)
(2)小张任意走了一条从甲学校到丙学校的线路,求小张恰好经过了 线路的概率是多少? (3分)
线路的概率是多少? (3分)
[答案]解:(1)利用列表或树状图的方法表示从甲校到丙校的线路所有可能出现的结果如下:
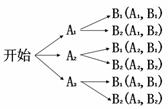
|
|
A1 |
A2 |
A3 |
|
B1 |
(A1 、B1) |
(A2 、B1) |
(A3、B1) |
|
B2 |
(A1 、 B2) |
(A2、 B2) |
(A3 、B2 ) |
(2) 小张从甲学校到丙学校共有6条不同的线路,其中经过B1线路有3条,
所以:P(小张恰好经过了 线路的概率)=
线路的概率)= .·
.·
36. (2011贵州贵阳,19,10分)
一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字3、4、5、
x.甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复试验.试验数据如下表:
|
摸球总次数 |
10 |
20 |
30 |
60 |
90 |
120 |
180 |
240 |
330 |
450 |
|
“和为8”出现的频数 |
2 |
10 |
13 |
24 |
30 |
37 |
58 |
82 |
110 |
150 |
|
“和为8”出现的频率 |
0.20 |
0.50 |
0.43 |
0.40 |
0.33 |
0.31 |
0.32 |
0.34 |
0.33 |
0.33 |
解答下列问题:
(1)如果实验继续进行下去,根据上表数据,出现“和为8”的频率将稳定在它的概率附近.估计出现“和为8”的概率是______;(4分)
(2)如果摸出的这两个小球上数字之和为9的概率是,那么x的值可以取7吗?请用列表法或画树状图法说明理由;如果x的值不可以取7,请写出一个符合要求的x值.(6分)
[答案]解:(1)0.33.
(2)x不可以取7,画树状图法说明如下:

从图中可知,数字和为9的概率为=.
当x=6时,摸出的两个小球上数字之和为9.
35. (2011湖北黄石,21,8分)2011年6月4日,李娜获得法网公开赛的冠军,圆了中国人的网球梦,也在国内掀起一股网球热,某市准备为青少年举行一次网球知识讲座,小明和妹妹都是网球迷,要求爸爸去买门票,但爸爸只买回一张门票,那么谁去就成了问题,小明想到一个办法:他拿出一个装有质地、大小相同的2x个红球与3x个白球的袋子,让爸爸从中摸出一个球,如果摸出的是红球,妹妹去听讲座,如果摸到的是白球,小明听讲座。
(1)爸爸说这个办法不公平,请你用概率的知识解释原因。
(2)若爸爸从袋中取出3个白球,再用小明提出的办法来确定谁去听讲座,请问摸球的结果是对小明有利还是对妹妹有利,说明理由。
[答案]解:(1)∵P(小明胜)= ,P(妹妹胜)=
,P(妹妹胜)=
∴P(小明胜)≠P(妹妹胜)
∴这个办法不公平
(2)3x-3=2x
X=3
∴当x>3时对小明有利
当x<3时对妹妹有利
当x=3时游戏公平
34. (2011湖北黄冈,19,7分)有3张扑克牌,分别是红桃3、红桃4和黑桃5.把牌洗匀后甲先抽取一张,记下花色和数字后将牌放回,洗匀后乙再抽取一张.
⑴先后两次抽得的数字分别记为s和t,则︱s-t︱≥1的概率.
⑵甲、乙两人做游戏,现有两种方案.A方案:若两次抽得相同花色则甲胜,否则乙胜.B方案:若两次抽得数字和为奇数则甲胜,否则乙胜.
请问甲选择哪种方案胜率更高?
[答案]⑴ ⑵A方案P(甲胜)=
⑵A方案P(甲胜)= ,B方案P(甲胜)=
,B方案P(甲胜)= 故选择A方案甲的胜率更高.
故选择A方案甲的胜率更高.
33. (2011湖北黄冈,17,6分)为了加强食品安全管理,有关部门对某大型超市的甲、乙两种品牌食用油共抽取18瓶进行检测,检测结果分成“优秀”、“合格”、“不合格”三个等级,数据处理后制成以下折线统计图和扇形统计图.
⑴甲、乙两种品牌食用油各被抽取了多少瓶用于检测?
⑵在该超市购买一瓶乙品牌食用油,请估计能买到“优秀”等级的概率是多少?


[答案]⑴(由不合格瓶数为1知道甲不合格的瓶数为1)甲、乙分别被抽取了10瓶、8瓶
⑵P(优秀)=
32. (2011湖北武汉市,20,7分)(本题满分7分)经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转.如果这三种可能性大小相同,现有两辆汽车经过这个十字路口.
(1)试用树形图或列表法中的一种列举出这两辆汽车行驶方向所有可能的结果;
(2)求至少有一辆汽车向左转的概率.
[答案]解法1:
(1)根据题意,可以画出如下的“树形图”: 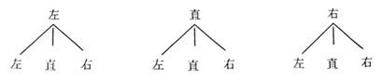
∴这两辆汽车行驶方向共有9种可能的结果
(2)由(1)中“树形图”知,至少有一辆汽车向左转的结果有5种,且所有结果的可能性相等
∴P(至少有一辆汽车向左转)=5/9
解法2:根据题意,可以列出如下的表格:
|
|
左 |
直 |
右 |
|
左 |
(左,左) |
(左,直) |
(左,右) |
|
直 |
(直,左) |
(直,直) |
(直,右) |
|
右 |
(右,左) |
(右,直) |
(右,右) |
以下同解法1(略)
31. (2011江苏无锡,22,7分)(本题满分7分)一不透明的袋子中装有4个球,它们除了上面分别标有的号码1、2、3、4不同外,其余均相同。将小球搅匀,并从袋中任意取出一球后放回;再将小球搅匀,并从袋中再任意取出一球。求第二次取出球的号码比第一次的大的概率。(请用“画树状图”或“列表”的方法给出分析过程,并写出结果)
 [答案].解:(1)树状图: 第一次
第二次
列表:
[答案].解:(1)树状图: 第一次
第二次
列表:
|
树状图或列表正确 …………………………(4分)
∴第一次与第二次的号码组合共有16种不同的情况,其中第二次取出球的号码比第一次的大的情况有6种,故第二次球的号码比第一次的大的概率是 = .…………………………………………………(7分)
30. (2011四川凉山州,22,8分)6张不透明的卡片,除正面画有不同的图形外,其它均相同,把这6张卡片洗匀后,正面向下放在桌上,另外还有与卡片上图形形状完全相同的地板砖若干块,所有地板砖的长都相等。
⑴从这6张卡片中随机抽取一张,与卡片上图形形状相对应的这种地板砖能进行平面镶嵌的概率是多少?
⑵从这6张卡片中随机抽取2张,利用列表或画树状图计算:与卡片上图形形状相对应的这两种地板砖能进行平面镶嵌的概率是多少?


[答案]
解:⑴
⑵根据题意得:
|
|
A |
B |
C |
D |
E |
F |
 A A |
|
AB |
AC |
AD |
AE |
AF |
|
B |
BA |
|
BC |
BD |
BE |
BF |
|
C |
CA |
CB |
|
CD |
CE |
CF |
|
D |
DA |
DB |
DC |
|
DE |
DE |
|
F |
EA |
EB |
EC |
ED |
|
EF |
|
|
FA |
FB |
FC |
FD |
FE |
|
由上表可知,共有30种可能的结果,且每种结果的可能性相同,其中能进行平面镶嵌的结果有8种,分别是:AB, AD, BE, CF, BA, DA, EB, FC 。

29. (2011四川乐山22,10分)在一个不透明的口袋里装有四个分别标有1、2、3、4的小球,它们的形状、大小等完全相同。小明先从口袋里随机不放回地取出一个小球,记下数字为x;小红在剩下有三个小球中随机取出一个小球,记下数字y。
(1)计算由x、y确定的点(x,y)在函数 图象上的概率;
图象上的概率;
(2)小明、小红约定做一个游戏,其规则是:若x、y满足xy>6,则小明胜;若x、y满足xy<6,则小红胜.这个游戏规则公平吗?说明理由;若不公平,怎样修改游戏规则才对双方公平?
[答案]
解:⑴.列表如下
|
X+Y |
1 |
2 |
3 |
4 |
|
1 |
- |
3 |
4 |
5 |
|
2 |
3 |
- |
5 |
6 |
|
3 |
4 |
5 |
- |
7 |
|
4 |
5 |
6 |
7 |
- |
∴
⑵列表如下
|
X·Y |
1 |
2 |
3 |
4 |
|
1 |
- |
2 |
3 |
4 |
|
2 |
2 |
- |
6 |
8 |
|
3 |
3 |
6 |
- |
12 |
|
4 |
4 |
8 |
12 |
- |
∵ ,
,
∴
∴这个游戏规则不公平
规则改为:“若x、y满足 ,则小明胜;若x、y满足
,则小明胜;若x、y满足 ,则小红胜”
,则小红胜”
∵ ,
,
∴
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com