
题目列表(包括答案和解析)
6.已知平面上一点M(5,0),若直线上存在点P使|PM|=4,则称该直线为“切割型直线”,下列直线中是“切割型直线”的是( )
①y=x+1;②y=2;③y=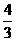 x;④y=2x+1.
x;④y=2x+1.
A.①③ B.①②
C.②③ D.③④
解析:根据题意,看所给直线上的点到定点M距离能否取4.可通过求各直线上的点到点M的最小距离,即点M到直线的距离来分析.①d=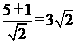 >4,故直线上不存在点到M距离等于4,不是“切割型直线”;②d=2<4,所以在直线上可以找到两个不同的点,使之到点M距离等于4,是“切割型直线”;③d=
>4,故直线上不存在点到M距离等于4,不是“切割型直线”;②d=2<4,所以在直线上可以找到两个不同的点,使之到点M距离等于4,是“切割型直线”;③d=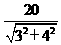 =4,直线上存在一点,使之到点M距离等于4,是“切割型直线”;④d=
=4,直线上存在一点,使之到点M距离等于4,是“切割型直线”;④d=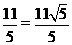 >4,故直线上不存在到点M距离等于4,不是“切割型直线”.
>4,故直线上不存在到点M距离等于4,不是“切割型直线”.
答案:C
5.下列命题中:
①两条直线互相平行等价于它们的斜率相等而截距不等;
②方程(2x+y-3)+λ(x-y+2)=0(λ为常数)表示经过两直线2x+y-3=0与x-y+2=0交点的所有直线;
③过点M(x0,y0),且与直线ax+bx+c=0(ab≠0)平行的直线的方程是a(x-x0)+b(y-y0)=0;
④两条平行直线3x-2y+5=0与6x-4y+8=0间的距离是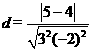 .
.
其中不正确的命题的个数是( )
A.0个 B.1个
C.2个 D.3个
解析:当斜率不存在时①不正确;方程(2x+y-3)+λ(x-y+2)=0不表示过交点的直线x-y+2=0,所以②不正确;若M(x0,y0)在直线ax+by+c=0上,则c=-ax0-by0,此时方程a(x-x0)+b(y-y0)=0将会重合于直线ax+by+c=0,所以③也不正确;只有④正确.
答案:D
4.使三条直线4x+y=4,mx+y=0,2x-3my=4不能围成三角形的m值最多有( )
A.1个 B.2个
C.3个 D.4个
解析:要使三条直线不能围成三角形,只需其中两条直线平行或者三条直线共点即可.
若4x+y=4与mx+y=0平行,则m=4;
若4x+y=4与2x-3my=4平行,则m=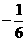 ;
;
若mx+y=0与2x-3my=4平行,则m值不存在;
若4x+y=4与mx+y=0及2x-3my=4共点,
则m=-1或m=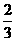 .
.
综上可知,m值最多有4个,故应选D.
答案:D
3.曲线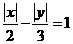 与直线y=2x+m有两个交点,则m的取值范围是( )
与直线y=2x+m有两个交点,则m的取值范围是( )
A.m>4或m<-4 B.-4<m<4
C.m>3或m<-3 D.-3<m<3
解析:曲线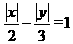 的图象如图所示.与直线y=2x+m有两个交点.则m>4或m<-4.故选A.
的图象如图所示.与直线y=2x+m有两个交点.则m>4或m<-4.故选A.
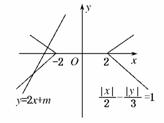
答案:A
2.入射光线沿直线x-2y+3=0射向直线l:y=x,被直线l反射后的光线所在直线的方程是( )
A.2x+y-3=0 B.2x-y-3=0
C.2x+y+3=0 D.2x-y+3=0
解析:由入射光线与反射光线所在直线关于直线l:y=x对称,把直线x-2y+3=0中的x,y互换,得到2x-y-3=0.
∴反射光线的方程为2x-y-3=0.故应选B.
答案:B
1.过点(-1,3)且垂直于直线x-2y+3=0的直线方程为( )
A.2x+y-1=0 B.2x+y-5=0
C.x+2y-5=0 D.x-2y+7=0
解析:已知直线的斜率为\f(1,2),且所求直线垂直于已知直线,所以所求直线的斜率为-2,故方程为y-3=-2(x+1),即2x+y-1=0.故选A.
答案:A
13.一束光线通过点M(25,18)射到x轴上,被反射到圆C:x2+(y-7)2=25上.
(1)求通过圆心的反射光线方程;
(2)求在x轴上入射点A的活动范围.
解:∵圆心C(0,7),半径r=5,
(1)M关于x轴的对称点N(25,-18),由光的性质可知,过圆心的反射光线所在的直线就是过N、C两点的直线,则过N、C的直线方程x+y-7=0,即为所求.
(2)设过N的直线方程为y+18=k(x-25),即kx-y-25k-18=0,当它为圆C的切线时,由=5⇒k=-或k=-.
∴过N与圆C相切的直线为y+18=-(x-25)或y+18=-(x-25),令y=0,得x=或x=1,
∵A点活动范围在两切线与x轴的两交点之间,
∴A点在x轴上的活动范围是.
12.设点C为曲线y=(x>0)上任一点,以点C为圆心的圆与x轴交于点E、A,与y轴交于点E、B.
(1)证明:多边形EACB的面积是定值,并求这个定值;
(2)设直线y=-2x+4与圆C交于点M,N,若|EM|=|EN|,求圆C的方程.
解:(1)证明:设点C(t>0),因为以点C为圆心的圆与x轴交于点E、A,与y轴交于点E、B.
所以,点E是直角坐标系原点,即E(0,0).
于是圆C的方程是(x-t)2+2=t2+.
则A(2t,0),B.
由|CE|=|CA|=|CB|知,圆心C在Rt△AEB的斜边AB上,于是多边形EACB为Rt△AEB,
其面积S=|EA|·|EB|=×2t×=4.
所以多边形EACB的面积是定值,这个定值是4.
(2)若|EM|=|EN|,则E在MN的垂直平分线上,即EC是MN的垂直平分线.
因为kEC==,kMN=-2.
所以由kEC·kMN=-1得t=2.
所以圆C的方程是(x-2)2+(y-1)2=5.
11.求过直线2x+y+4=0和圆x2+y2+2x-4y+1=0的交点,且满足下列条件之一的圆的方程.
(1)过原点;(2)有最小面积.
分析:可考虑利用过直线与圆的交点的圆系方程来解决问题.
解:(1)设所求圆的方程为
x2+y2+2x-4y+1+λ(2x+y+4)=0,
即x2+y2+2(1+λ)x+(λ-4)y+(1+4λ)=0. ①
∵此圆过原点,∴1+4λ=0,λ=-.
故所求圆的方程为x2+y2+x-y=0.
(2)解法一:当半径最小时,圆面积也最小,对方程①左边配方,得
2+2
=2+≥.
∴当λ=时,此圆面积最小,故满足条件的圆的方程为2+2=.
解法二:当圆心在直线2x+y+4=0上时,圆面积最小,易求得圆心坐标为,代入直线方程得-2(1+λ)-+4=0,解得λ=.
∴当λ=时,此圆面积最小.故满足条件的圆的方程为x2+y2+x-y+=0.
评析:联立直线与圆的方程,通过解方程组求出交点坐标.进而求出圆的方程计算繁琐.
过直线与圆交点的圆系方程
设直线l:Ax+By+C=0与圆C:x2+y2+Dx+Ey+F=0相交,则方程x2+y2+Dx+Ey+F+λ(Ax+By+C)=0表示过直线l与圆C的交点的圆系方程.
10.设有一组圆:Ck:(x-k+1)2+(y-3k)2=2k4(k∈N*).下列四个命题:
(1)存在一条定直线与所有的圆均相切
(2)存在一条定直线与所有的圆均相交
(3)存在一条定直线与所有的圆均不相交
(4)所有的圆均不经过原点
其中真命题的序号是____________.(写出所有真命题的序号)
解析:设直线为y=ax+b,
d==.
∵d中无二次项,∴不存在定值a、b使d=k2,(1)错误,
当a=3,b=3时,
d=0,恒小于k2与圆相交,(2)正确.
同(1)项之理,(3)错误.
将O(0,0)代入,方程不成立,(4)正确,选(2)(4).
答案:(2)(4)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com