
题目列表(包括答案和解析)
5.给定两个向量a=(3,4),b=(2,1),若(a+xb)⊥(a-b),则x的值等于
A.-3 B.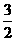
C.3
D.-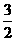
4. 某地区高中分三类,A类校共有学生4000人,B类校共有学生2000人,C类校共有学生3000人.现欲抽样分析某次考试的情况,若抽取900份试卷进行分析,则从A类校抽取的试卷份数应为
A.450 B.400
C.300 D.200
3.函数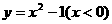 的反函数是
的反函数是
A.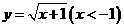 B.
B.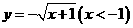
C.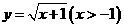 D.
D.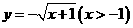
2.已知θ∈[0,π],f(θ)=sin(cosθ)的最大值为a,最小值为b,g(θ)=cos(sinθ)的最大值为c,最小值为d,则a、b、c、d从小到大的顺序为
A.b<d<a<c B.d<b<c<a
C.b<d<c<a D.d<b<a<c
1. 已知二次函数f(x)=(x-a)(x-b)-2(a<b),并且α、β(α<β)是方程f(x)=0的两根,则a、b、α、β的大小关系是
A.α<a<b<β B.a<α<β<b
C.a<α<b<β D.α<a<β<b
14.(14分)设复数z满足|z|=5,且(3+4i)z在复平面上对应的点在第二、四象限的角平分线上,|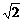 z-m|=5
z-m|=5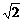 (m∈R),求z和m的值.
(m∈R),求z和m的值.
解:设出z的代数形式z=x+yi(x、y∈R).
∵|z|=5,∴x2+y2=25.
∵(3+4i)z=(3+4i)(x+yi)
=(3x-4y)+(4x+3y)i,
又(3+4i)z在复平面内对应的点在第二、四象限的角平分线上,则它的实部与虚部互为相反数,∴3x-4y+4x+3y=0.
化简得y=7x.将其代入x2+y2=25,得x=±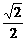 ,y=±
,y=±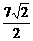 .
.
∴z=±(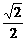 +
+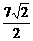 i).则当z=
i).则当z=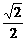 +
+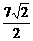 i时,
i时,
|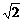 z-m|=|1+7i-m|=5
z-m|=|1+7i-m|=5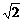 ,
,
即(1-m)2+72=50.解得m=0或m=2.
当z=-(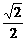 +
+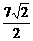 i)时,同理可得m=0或m=-2.
i)时,同理可得m=0或m=-2.
13.(14分)非零复数a、b、c满足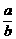 =
=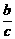 =
=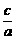 ,求
,求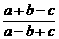 的值.
的值.
解:设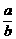 =
=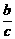 =
=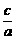 =k,则a=bk,b=ck,c=ak,即c=ak,b=ak·k=ak2,a=ak2·k=ak3,
=k,则a=bk,b=ck,c=ak,即c=ak,b=ak·k=ak2,a=ak2·k=ak3,
∴k3=1.∴k=1或k=-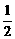 ±
±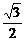 i.
i.
则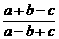 =
=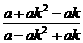 =
=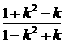 .
.
若k=1,则原式=1;
若k=-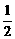 +
+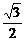 i,则原式=-
i,则原式=-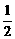 -
-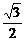 i;
i;
若k=-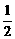 -
-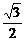 i,则原式=-
i,则原式=-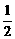 +
+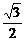 i.
i.
综上,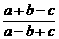 的值分别为1,-
的值分别为1,-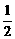 -
-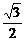 i,-1+
i,-1+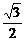 i.
i.
12.(14分)设复数z满足4z+2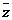 =3
=3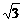 +i,ω=sinθ-icosθ(θ∈R),求z的值和|z-ω|的取值范围.
+i,ω=sinθ-icosθ(θ∈R),求z的值和|z-ω|的取值范围.
解:设z=a+bi(a、b∈R),则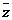 =a-bi,代入4z+2
=a-bi,代入4z+2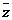 =3
=3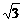 +i,得
+i,得
4(a+bi)+2(a-bi)=3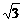 +i,
+i,
即6a+2bi=3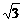 +i.
+i.
∴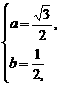 ∴z=
∴z=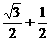 i.
i.
|z-ω|=|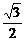 +
+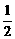 i-(sinθ-icosθ)|
i-(sinθ-icosθ)|
=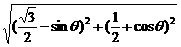
=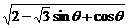 =
=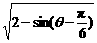 .
.
∵-1≤sin(θ-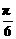 )≤1,∴0≤2-2sin(θ-
)≤1,∴0≤2-2sin(θ-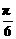 )≤4.∴0≤|z-ω|≤2.
)≤4.∴0≤|z-ω|≤2.
11.(12分)设复数z1、z2满足z1·z2+2iz1-2iz2+1=0,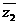 -z1=2i,求z1和z2.
-z1=2i,求z1和z2.
解:∵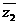 -z1=2i,∴
-z1=2i,∴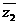 =z1+2i.
=z1+2i.
∴z2=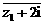 ,即z2=
,即z2=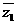 -2i.
-2i.
又∵z1·z2+2iz1-2iz2+1=0,
∴z1(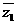 -2i)+2iz1-2i(
-2i)+2iz1-2i(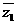 -2i)+1=0,
-2i)+1=0,
即|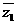 |2-2i
|2-2i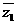 -3=0.
-3=0.
令z1=a+bi(a、b∈R),
得a2+b2-2b-3-2ai=0,
即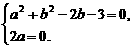 解得
解得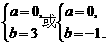
∴z1=3i,z2=-5i或z1=-i,z2=-i.
10.复数z满足z·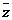 +z+
+z+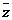 =3,则z对应点的轨迹是____________.
=3,则z对应点的轨迹是____________.
解析:设z=x+yi(x、y∈R),则x2+y2+2x=3表示圆.
答案:以点(-1,0)为圆心,2为半径的圆
三、解答题(本大题共4小题,共54分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com