
题目列表(包括答案和解析)
8、方程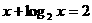 和
和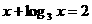 的根分别是
的根分别是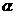 、
、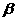 ,则有( )
,则有( )
A. 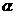 <
<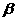 B.
B. 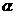 >
>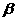 C.
C. 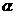 =
=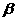 D. 无法确定
D. 无法确定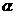 与
与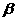 的大小
的大小
7、设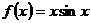 ,
,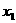 、
、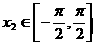 ,且
,且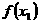 >
>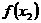 ,则下列结论必成立的是( )
,则下列结论必成立的是( )
A. 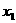 >
>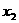 B.
B. 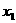 +
+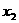 >0 C.
>0 C. 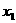 <
<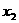 D.
D. 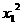 >
>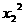
6、函数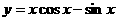 在下面的哪个区间上是增函数( )
在下面的哪个区间上是增函数( )
A. 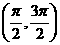 B.
B.
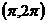 C.
C.
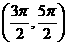 D.
D. 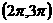
5、已知函数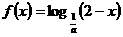 在其定义域上单调递减,则函数
在其定义域上单调递减,则函数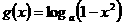 的单调减区间是( )
的单调减区间是( )
A. 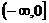 B.
B. 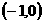 C.
C.
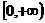 D.
D.
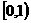
4、将函数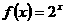 的图象向左平移一个单位得到图象
的图象向左平移一个单位得到图象 ,再将
,再将 向上平移一个单位得图象
向上平移一个单位得图象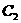 ,作出
,作出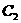 关于直线
关于直线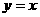 对称的图象
对称的图象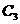 ,则
,则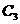 对应的函数的解析式为( )
对应的函数的解析式为( )
A. 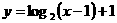 B.
B.
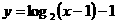
C. 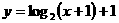 D.
D.
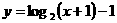
3、已知0<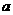 <1,
<1,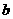 <-1,则函数
<-1,则函数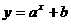 的图象必定不经过( )
的图象必定不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2、已知函数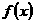 的定义域为[0,1],值域为[1,2],则函数
的定义域为[0,1],值域为[1,2],则函数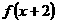 的定义域和值域分别是( )
的定义域和值域分别是( )
A. [0,1] ,[1,2] B. [2,3] ,[3,4] C. [-2,-1] ,[1,2] D. [-1,2] ,[3,4]
1、已知函数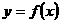 ,
,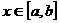 ,那么集合
,那么集合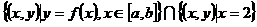 中元素的个数为( )
中元素的个数为( )
A. 1 B. 0 C. 1或0 D. 1或2
44、购买一件售价为5000元的商品,采用分期付款方法.每期付款数相同,购买后1个月付款一次,过1个月再付一次,如此下去,到第12次付款后全部付清.如果月利率为0.8%,每月利息按复利算(上月利息要计入下月本金),那么每期应付款多少(精确到1元)?
解:设每期付款x元,根据题意,得到
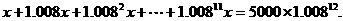
所以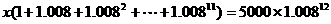 .
.
由等比数列前n项和的公式得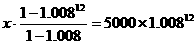
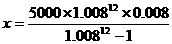 ,由计算器算得x≈439(元).
,由计算器算得x≈439(元).
答:每期应付款约439元.
解法二:设每期付款x元,第n期后欠款数记作an那么,
第1期后的欠款数为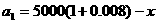
第2期后的欠款数为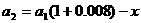
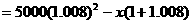
第3期后的欠款数为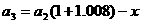
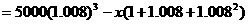 .
.
……
第12期后的欠款数为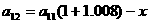
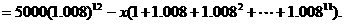
因为第12期全部付清,所以a12=0即
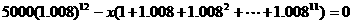 ,
,
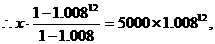
解得 x≈439(元).
答:每期应付款约439元.
43、某乡镇现在人均一年占有粮食360千克,如果该乡镇人口平均每年增长1.2%,粮食总产量平均每年增长4%,那么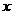 年后若人均一年占有
年后若人均一年占有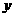 千克粮食,求出函数
千克粮食,求出函数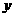 关于
关于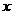 的解析式。
的解析式。
分析:此题解决的关键在于恰当引入变量,抓准数量关系,并转化成数学表达式,具体解答可以依照例子。
解:设该乡镇现在人口量为M,则该乡镇现在一年的粮食总产量为360M。
经过1年后
该乡镇粮食总产量为360M(1+4%),
人口量为M(1+1.2%)
则人均占有粮食为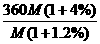 ;
;
经过2年后:人均占有粮食为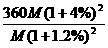 ……
……
经过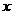 年后:人均占有粮食
年后:人均占有粮食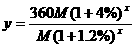
即所求函数式为: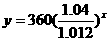
评述:这是一个有关平均增长率的问题,如果原来的产值的基础数为N,平均增长率为P,则对于时间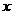 的总产值
的总产值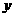 可以用下面的公式,即
可以用下面的公式,即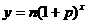
解决平均增长率的问题,常用这个函数式。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com