
题目列表(包括答案和解析)
21.(本小题满分12分)
已知函数f(x)=-x3+ax2+bx在区间(-2,1)内,当x=-1时取得极小值,x=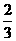 时取得极大值.求:
时取得极大值.求:
(1)函数y=f(x)在x=-2时的对应点的切线方程;
(2)函数f(x)在[-2,1]上的最大值与最小值.
20.(本小题满分12分)
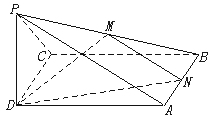
如图,已知正四棱锥P-ABCD的底面为边长是a的正方形,PD⊥底面ABCD,设PD=6,M,N分别为PB,AB的中点.求:
(1)三棱锥P-DMN的体积;
(2)二面角M-DN-C的平面角的正切值.
19.(本小题满分12分)
 设有两门高射炮,每一门击中飞机的概率为0.6,用这两门炮同时发射一发炮弹击中飞机的概率为多少?又若有一架敌机入侵领空,欲以99%以上的概率击中它,问至少需要多少门这样的高射炮?
设有两门高射炮,每一门击中飞机的概率为0.6,用这两门炮同时发射一发炮弹击中飞机的概率为多少?又若有一架敌机入侵领空,欲以99%以上的概率击中它,问至少需要多少门这样的高射炮?
18.(本小题满分12分)
已知数列{an}为等差数列,{bn}为等比数列,且b1=a12,b2=a22,b3=a32(a1<a2),q为等比数列的公比,又|q|<1.求:
(1)等比数列的公比q;
(2)又若a1=-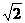 时,等差数列的前10项和为多少?
时,等差数列的前10项和为多少?
17.(本小题满分12分)
已知函数f(x)=Asinωx+Bcosωx(其中A,B,ω为实常数,且ω>0)的最小正周期为2,并且当x=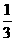 时,f(x)的最大值为2.
时,f(x)的最大值为2.
(1)求函数f(x)的表达式;
(2)在区间[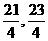 ]上函数f(x)存在对称轴,求此对称轴方程.
]上函数f(x)存在对称轴,求此对称轴方程.
16.对于定义在R上的函数f(x),若实数x0满足f(x0)=x0,则称x0是函数f(x)的一个不动点,现给定一个实数a∈(4,5),则函数f(x)=x2+ax+1的不动点共有________个.
15.已知函数f(x)=log3x+2,x∈[1,9],则函数y=[f(x)]2+f(x2)的值域是________.
14.设y=f(x)是二次函数,方程f(x)=0有两个相等实根且f '(x)=2x+2,则y=f(x)的表达式是________.
13.化简(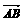 -
-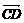 )-(
)-(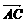 -
-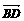 )=________.
)=________.
12.用一张钢板制作一个容积为4 m3的无盖长方体水箱,可用的长方形钢板有四种不同的规格(长×宽的尺寸如选项所示,单位为m).若既要够用,又要所剩最少,则应选择钢板的规格是
A.2×5 B.2×2.5 C.2×6.1 D.3×5
第Ⅱ卷(非选择题 共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com