
题目列表(包括答案和解析)
10.(2010全国卷1理)(22)(本小题满分12分)(注意:在试题卷上作答无效)
已知数列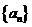 中,
中, .
.
(Ⅰ)设 ,求数列
,求数列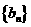 的通项公式;
的通项公式;
(Ⅱ)求使不等式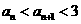 成立的
成立的 的取值范围 .
的取值范围 .


9.(2010四川理)(21)(本小题满分12分)
已知数列{an}满足a1=0,a2=2,且对任意m、n∈N*都有
a2m-1+a2n-1=2am+n-1+2(m-n)2
(Ⅰ)求a3,a5;
(Ⅱ)设bn=a2n+1-a2n-1(n∈N*),证明:{bn}是等差数列;
(Ⅲ)设cn=(an+1-an)qn-1(q≠0,n∈N*),求数列{cn}的前n项和Sn.
本小题主要考查数列的基础知识和化归、分类整合等数学思想,以及推理论证、分析与解决问题的能力.
解:(1)由题意,零m=2,n-1,可得a3=2a2-a1+2=6
再令m=3,n=1,可得a5=2a3-a1+8=20………………………………2分
(2)当n∈N *时,由已知(以n+2代替m)可得
a2n+3+a2n-1=2a2n+1+8
于是[a2(n+1)+1-a2(n+1)-1]-(a2n+1-a2n-1)=8
即 bn+1-bn=8
所以{bn}是公差为8的等差数列………………………………………………5分
(3)由(1)(2)解答可知{bn}是首项为b1=a3-a1=6,公差为8的等差数列
则bn=8n-2,即a2n+=1-a2n-1=8n-2
另由已知(令m=1)可得
an=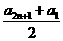 -(n-1)2.
-(n-1)2.
那么an+1-an=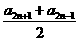 -2n+1
-2n+1
= -2n+1
-2n+1
=2n
于是cn=2nqn-1.
当q=1时,Sn=2+4+6+……+2n=n(n+1)
当q≠1时,Sn=2·q0+4·q1+6·q2+……+2n·qn-1.
两边同乘以q,可得
qSn=2·q1+4·q2+6·q3+……+2n·qn.
上述两式相减得
(1-q)Sn=2(1+q+q2+……+qn-1)-2nqn
=2·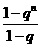 -2nqn
-2nqn
=2·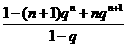
所以Sn=2·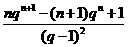
综上所述,Sn=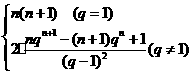 …………………………12分
…………………………12分
8.(2010北京文)(16)(本小题共13分)
已知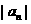 为等差数列,且
为等差数列,且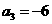 ,
, 。
。
(Ⅰ)求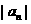 的通项公式;
的通项公式;
(Ⅱ)若等差数列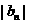 满足
满足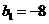 ,
, ,求
,求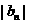 的前n项和公式
的前n项和公式
解:(Ⅰ)设等差数列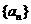 的公差
的公差 。
。
因为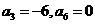
所以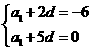 解得
解得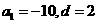
所以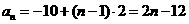
(Ⅱ)设等比数列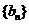 的公比为
的公比为
因为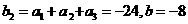
所以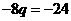 即
即 =3
=3
所以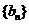 的前
的前 项和公式为
项和公式为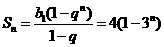
7.(2010浙江文)(19)(本题满分14分)设a1,d为实数,首项为a1,公差为d的等差数列{an}的前n项和为Sn,满足 +15=0。
+15=0。
(Ⅰ)若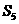 =5,求
=5,求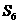 及a1;
及a1;
(Ⅱ)求d的取值范围。

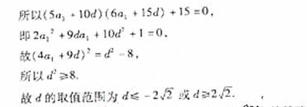
6.(2010重庆文)(16)(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分. )
已知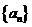 是首项为19,公差为-2的等差数列,
是首项为19,公差为-2的等差数列,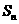 为
为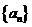 的前
的前 项和.
项和.
(Ⅰ)求通项 及
及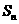 ;
;
(Ⅱ)设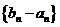 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列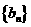 的通项公式及其前
的通项公式及其前 项和
项和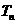 .
.

5.(2010安徽文)(21)(本小题满分13分)
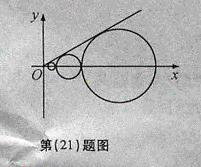 设
设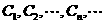 是坐标平面上的一列圆,它们的圆心都在
是坐标平面上的一列圆,它们的圆心都在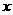 轴的正半轴上,且都与直线
轴的正半轴上,且都与直线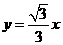 相切,对每一个正整数
相切,对每一个正整数 ,圆
,圆 都与圆
都与圆 相互外切,以
相互外切,以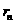 表示
表示 的半径,已知
的半径,已知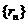 为递增数列.
为递增数列.
(Ⅰ)证明: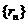 为等比数列;
为等比数列;
(Ⅱ)设 ,求数列
,求数列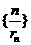 的前
的前 项和.
项和.
[命题意图]本题考查等比列的基本知识,利用错位相减法求和等基本方法,考察抽象概括能力以及推理论证能力.
[解题指导](1)求直线倾斜角的正弦,设 的圆心为
的圆心为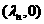 ,得
,得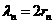 ,同理得
,同理得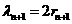 ,结合两圆相切得圆心距与半径间的关系,得两圆半径之间的关系,即
,结合两圆相切得圆心距与半径间的关系,得两圆半径之间的关系,即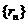 中
中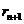 与
与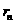 的关系,证明
的关系,证明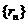 为等比数列;(2)利用(1)的结论求
为等比数列;(2)利用(1)的结论求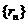 的通项公式,代入数列
的通项公式,代入数列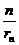 ,然后用错位相减法求和.
,然后用错位相减法求和.

[方法技巧]对于数列与几何图形相结合的问题,通常利用几何知识,并结合图形,得出关于数列相邻项 与
与 之间的关系,然后根据这个递推关系,结合所求内容变形,得出通项公式或其他所求结论.对于数列求和问题,若数列的通项公式由等差与等比数列的积构成的数列时,通常是利用前n项和
之间的关系,然后根据这个递推关系,结合所求内容变形,得出通项公式或其他所求结论.对于数列求和问题,若数列的通项公式由等差与等比数列的积构成的数列时,通常是利用前n项和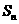 乘以公比,然后错位相减解决.
乘以公比,然后错位相减解决.
4.(2010江西理)22. (本小题满分14分)
证明以下命题:
(1) 对任一正整a,都存在整数b,c(b<c),使得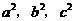 成等差数列。
成等差数列。
(2) 存在无穷多个互不相似的三角形△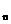 ,其边长
,其边长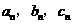 为正整数且
为正整数且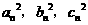 成等差数列。
成等差数列。
[解析]作为压轴题,考查数学综合分析问题的能力以及创新能力。
(1)考虑到结构要证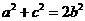 ,;类似勾股数进行拼凑。
,;类似勾股数进行拼凑。
证明:考虑到结构特征,取特值 满足等差数列,只需取b=5a,c=7a,对一切正整数a均能成立。
满足等差数列,只需取b=5a,c=7a,对一切正整数a均能成立。
结合第一问的特征,将等差数列分解,通过一个可做多种结构分解的因式说明构成三角形,再证明互不相似,且无穷。
证明:当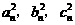 成等差数列,则
成等差数列,则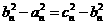 ,
,
分解得: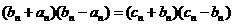
选取关于n的一个多项式,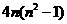 做两种途径的分解
做两种途径的分解
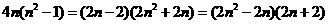
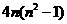
对比目标式,构造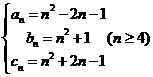 ,由第一问结论得,等差数列成立,
,由第一问结论得,等差数列成立,
考察三角形边长关系,可构成三角形的三边。
下证互不相似。
任取正整数m,n,若△m,△ 相似:则三边对应成比例
相似:则三边对应成比例 ,
,
由比例的性质得: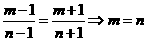 ,与约定不同的值矛盾,故互不相似。
,与约定不同的值矛盾,故互不相似。
3.(2010全国卷2文)(18)(本小题满分12分)
已知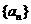 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且
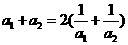 ,
,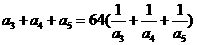
(Ⅰ)求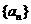 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列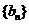 的前
的前 项和
项和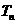 。
。
[解析]本题考查了数列通项、前 项和及方程与方程组的基础知识。
项和及方程与方程组的基础知识。
(1)设出公比根据条件列出关于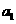 与
与 的方程求得
的方程求得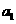 与
与 ,可求得数列的通项公式。
,可求得数列的通项公式。
(2)由(1)中求得数列通项公式,可求出bn的通项公式,由其通项公式化可知其和可分成两个等比数列分别求和即可求得。
2.(2010陕西文)16.(本小题满分12分)
已知{an}是公差不为零的等差数列,a1=1,且a1,a3,a9成等比数列.
(Ⅰ)求数列{an}的通项; (Ⅱ)求数列{2an}的前n项和Sn.
解 (Ⅰ)由题设知公差d≠0,
由a1=1,a1,a3,a9成等比数列得 =
= ,
,
解得d=1,d=0(舍去), 故{an}的通项an=1+(n-1)×1=n.
(Ⅱ)由(Ⅰ)知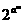 =2n,由等比数列前n项和公式得
=2n,由等比数列前n项和公式得
Sm=2+22+23+…+2n=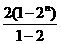 =2n+1-2.
=2n+1-2.
1.(2010上海文)21.(本题满分14分)本题共有2个小题,第一个小题满分6分,第2个小题满分8分。
已知数列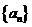 的前
的前 项和为
项和为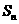 ,且
,且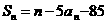 ,
,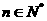
(1)证明: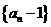 是等比数列;
是等比数列;
(2)求数列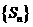 的通项公式,并求出使得
的通项公式,并求出使得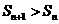 成立的最小正整数
成立的最小正整数 .
.
解析:(1) 当n=1时,a1=-14;当n≥2时,an=Sn-Sn-1=-5an+5an-1+1,所以 ,
又a1-1=-15≠0,所以数列{an-1}是等比数列;
(2) 由(1)知:
,
又a1-1=-15≠0,所以数列{an-1}是等比数列;
(2) 由(1)知: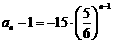 ,得
,得 ,从而
,从而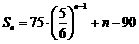 (nÎN*);
由Sn+1>Sn,得
(nÎN*);
由Sn+1>Sn,得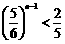 ,
,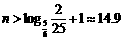 ,最小正整数n=15.
,最小正整数n=15.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com