
题目列表(包括答案和解析)
26.(2010福建理)7.若点O和点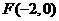 分别是双曲线
分别是双曲线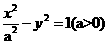 的中心和左焦点,点P为双曲线右支上的任意一点,则
的中心和左焦点,点P为双曲线右支上的任意一点,则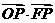 的取值范围为 ( )
的取值范围为 ( )
A.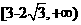 B.
B.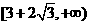 C.
C.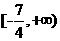 D.
D.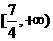
[答案]B
[解析]因为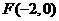 是已知双曲线的左焦点,所以
是已知双曲线的左焦点,所以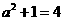 ,即
,即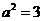 ,所以双曲线方程为
,所以双曲线方程为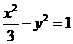 ,设点P
,设点P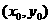 ,则有
,则有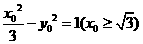 ,解得
,解得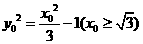 ,因为
,因为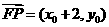 ,
,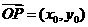 ,所以
,所以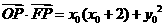 =
=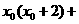
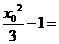
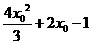 ,此二次函数对应的抛物线的对称轴为
,此二次函数对应的抛物线的对称轴为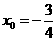 ,因为
,因为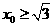 ,所以当
,所以当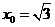 时,
时,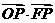 取得最小值
取得最小值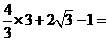
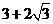 ,故
,故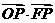 的取值范围是
的取值范围是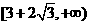 ,选B。
,选B。
[命题意图]本题考查待定系数法求双曲线方程,考查平面向量的数量积的坐标运算、二次函数的单调性与最值等,考查了同学们对基础知识的熟练程序以及知识的综合应用能力、运算能力。
25.(2010福建理)

A. ①④ B. ②③ C.②④ D.③④
[答案]C
[解析]经分析容易得出②④正确,故选C。
[命题意图]本题属新题型,考查函数的相关知识。
24.(2010湖北理数)9.若直线y=x+b与曲线 有公共点,则b的取值范围是
有公共点,则b的取值范围是
A. 
B. 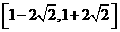
C. 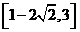
D. 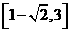
[答案]C
[解析]曲线方程可化简为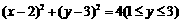 ,即表示圆心为(2,3)半径为2的半圆,依据数形结合,当直线
,即表示圆心为(2,3)半径为2的半圆,依据数形结合,当直线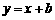 与此半圆相切时须满足圆心(2,3)到直线y=x+b距离等于2,解得
与此半圆相切时须满足圆心(2,3)到直线y=x+b距离等于2,解得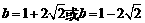 ,因为是下半圆故可得
,因为是下半圆故可得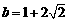 (舍),当直线过(0,3)时,解得b=3,故
(舍),当直线过(0,3)时,解得b=3,故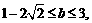 所以C正确.
所以C正确.
23.(2010安徽理)5、双曲线方程为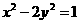 ,则它的右焦点坐标为
,则它的右焦点坐标为
A、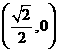 B、
B、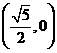 C、
C、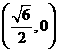 D、
D、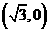
[答案]C
[解析]双曲线的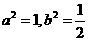 ,
,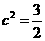 ,
,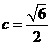 ,所以右焦点为
,所以右焦点为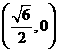 .
.
[误区警示]本题考查双曲线的交点,把双曲线方程先转化为标准方程,然后利用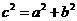 求出c即可得出交点坐标.但因方程不是标准形式,很多学生会误认为
求出c即可得出交点坐标.但因方程不是标准形式,很多学生会误认为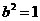 或
或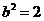 ,从而得出错误结论.
,从而得出错误结论.
22.(2010山东理)(7)由曲线y= ,y=
,y=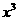 围成的封闭图形面积为
围成的封闭图形面积为
(A)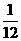 (B)
(B)
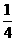 (C)
(C) 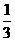 (D)
(D)
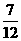
[答案]A
[解析]由题意得:所求封闭图形的面积为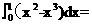
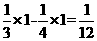 ,故选A。
,故选A。
[命题意图]本题考查定积分的基础知识,由定积分求曲线围成封闭图形的面积。
21.(2010湖北文)9.若直线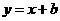 与曲线
与曲线 有公共点,则b的取值范围是
有公共点,则b的取值范围是
A.[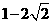 ,
,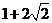 ] B.[
] B.[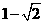 ,3]
,3]
C.[-1,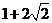 ] D.[
] D.[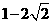 ,3]
,3]

20.(2010四川文)(3)抛物线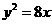 的焦点到准线的距离是
的焦点到准线的距离是
(A) 1 (B)2 (C)4 (D)8
[答案]C
[解析]由y2=2px=8x知p=4
又交点到准线的距离就是p
19.(2010四川文)(10)椭圆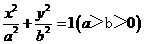 的右焦点为F,其右准线与
的右焦点为F,其右准线与 轴的交点为
轴的交点为 .在椭圆上存在点P满足线段AP的垂直平分线过点F,则椭圆离心率的取值范围是
.在椭圆上存在点P满足线段AP的垂直平分线过点F,则椭圆离心率的取值范围是
(A)(0,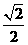 ] (B)(0,
] (B)(0, ] (C)[
] (C)[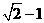 ,1)
(D)[
,1)
(D)[ ,1)
,1)
[答案]D
[解析]由题意,椭圆上存在点P,使得线段AP的垂直平分线过点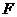 ,
,
即F点到P点与A点的距离相等
而|FA|=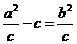
|PF|∈[a-c,a+c]
于是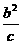 ∈[a-c,a+c]
∈[a-c,a+c]
即ac-c2≤b2≤ac+c2
∴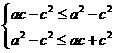
Þ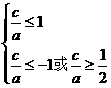
又e∈(0,1)
故e∈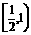
18.(2010全国卷1理)(9)已知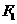 、
、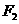 为双曲线C:
为双曲线C: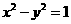 的左、右焦点,点P在C上,∠
的左、右焦点,点P在C上,∠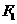 P
P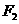 =
= ,则P到x轴的距离为
,则P到x轴的距离为
(A) 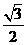 (B)
(B)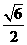 (C)
(C) 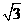 (D)
(D) 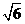
[答案] B

17.(2010全国卷1文)(8)已知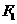 、
、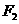 为双曲线C:
为双曲线C: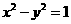 的左、右焦点,点P在C上,∠
的左、右焦点,点P在C上,∠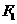
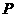
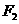 =
= ,则
,则
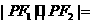
(A)2 (B)4 (C) 6 (D) 8
[答案]B
[命题意图]本小题主要考查双曲线定义、几何性质、余弦定理,考查转化的数学思想,通过本题可以有效地考查考生的综合运用能力及运算能力.
[解析1].由余弦定理得
cos∠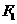 P
P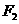 =
=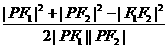
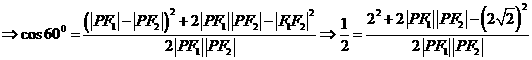
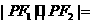 4
4
[解析2]由焦点三角形面积公式得:
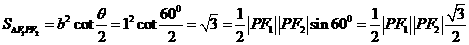
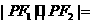 4
4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com