
题目列表(包括答案和解析)
2.(2010陕西文)11.观察下列等式:13+23=(1+2)2,13+23+33=(1+2+3)2,13+23+33+43=
(1+2+3+4)2,…,根据上述规律,第四个等式为13+23+33+43+53=(1+2+3+4+5)2(或152).
解析:第i个等式左边为1到i+1的立方和,右边为1到i+1和的完全平方
所以第四个等式为13+23+33+43+53=(1+2+3+4+5)2(或152).
1.(2010浙江理)(14)设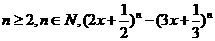
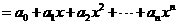 ,
,
将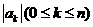 的最小值记为
的最小值记为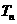 ,则
,则
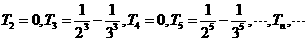
其中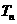 =__________________ .
=__________________ .
解析:本题主要考察了合情推理,利用归纳和类比进行简单的推理,属容易题
9.(2010福建理)3.设等差数列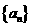 的前n项和为
的前n项和为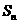 ,若
,若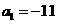 ,
,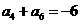 ,则当
,则当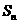 取最小值时,n等于
取最小值时,n等于
A.6 B.7 C.8 D.9
[答案]A
[解析]设该数列的公差为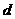 ,则
,则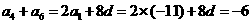 ,解得
,解得 ,
,
所以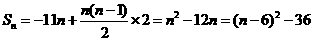 ,所以当
,所以当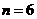 时,
时,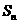 取最小值。
取最小值。
[命题意图]本题考查等差数列的通项公式以及前n项和公式的应用,考查二次函数最值的求法及计算能力。
8.(2010安徽理)10、设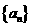 是任意等比数列,它的前
是任意等比数列,它的前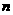 项和,前
项和,前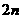 项和与前
项和与前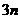 项和分别为
项和分别为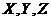 ,则下列等式中恒成立的是
,则下列等式中恒成立的是
A、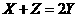 B、
B、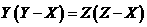
C、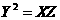 D、
D、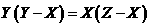
[答案] D
[分析]取等比数列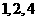 ,令
,令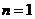 得
得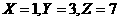 代入验算,只有选项D满足。
代入验算,只有选项D满足。
[方法技巧]对于含有较多字母的客观题,可以取满足条件的数字代替字母,代入验证,若能排除3个选项,剩下唯一正确的就一定正确;若不能完全排除,可以取其他数字验证继续排除.本题也可以首项、公比即项数n表示代入验证得结论.
(2010湖北理数)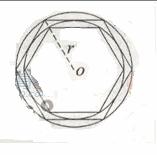 7、如图,在半径为r 的园内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去,设
7、如图,在半径为r 的园内作内接正六边形,再作正六边形的内切圆,又在此内切圆内作内接正六边形,如此无限继续下去,设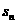 为前n个圆的面积之和,则
为前n个圆的面积之和,则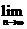
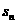 =
=
A. 2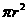 B.
B. 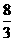
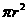 C.4
C.4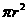 D.6
D.6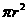

7.(2010湖北文)7.已知等比数列{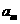 }中,各项都是正数,且
}中,各项都是正数,且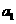 ,
,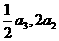 成等差数列,则
成等差数列,则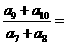
A.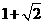 B.
B. 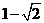 C.
C.
 D
D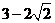
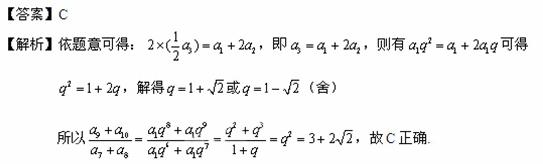
6.(2010全国卷1文)(4)已知各项均为正数的等比数列{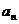 },
},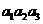 =5,
=5,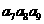 =10,则
=10,则
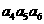 =
=
(A) 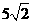 (B) 7 (C) 6 (D)
(B) 7 (C) 6 (D) 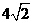
[答案]A
[命题意图]本小题主要考查等比数列的性质、指数幂的运算、根式与指数式的互化等知识,着重考查了转化与化归的数学思想.
[解析]由等比数列的性质知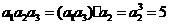 ,
,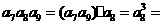 10,所以
10,所以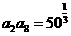 ,
,
所以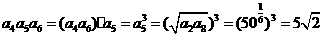
5.(2010天津理)(6)已知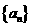 是首项为1的等比数列,
是首项为1的等比数列,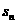 是
是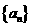 的前n项和,且
的前n项和,且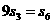 ,则数列
,则数列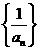 的前5项和为
的前5项和为
(A)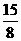 或5 (B)
或5 (B)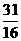 或5 (C)
或5 (C)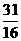 (D)
(D)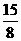
[答案]C
[解析]本题主要考查等比数列前n项和公式及等比数列的性质,属于中等题。
显然q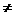 1,所以
1,所以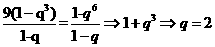 ,所以
,所以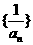 是首项为1,公比为
是首项为1,公比为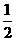 的等比数列,
前5项和
的等比数列,
前5项和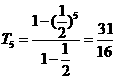 .
.
[温馨提示]在进行等比数列运算时要注意约分,降低幂的次数,同时也要注意基本量法的应用。
4.(2010四川理)(8)已知数列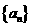 的首项
的首项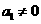 ,其前
,其前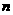 项的和为
项的和为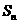 ,且
,且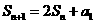 ,则
,则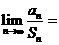
(A)0 (B)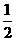 (C) 1
(D)2
(C) 1
(D)2
解析:由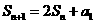 ,且
,且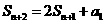
作差得an+2=2an+1
又S2=2S1+a1,即a2+a1=2a1+a1 Þ a2=2a1
故{an}是公比为2的等比数列
Sn=a1+2a1+22a1+……+2n-1a1=(2n-1)a1
则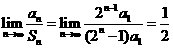
[答案]B
3.(2010北京理)(2)在等比数列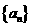 中,
中,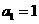 ,公比
,公比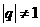 .若
.若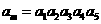 ,则m=
,则m=
(A)9 (B)10 (C)11 (D)12
[答案]C
2.(2010江西理)4. 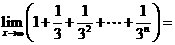 ( )
( )
A. 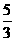 B.
B. 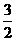 C. 2 D. 不存在
C. 2 D. 不存在
[答案]B
[解析]考查等比数列求和与极限知识.解法一:先求和,然后对和取极限。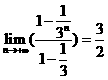
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com