
题目列表(包括答案和解析)
11.(本小题满分12分)
如图3,在正三棱柱ABC-
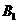
 中,AB=4,
A
中,AB=4,
A =
= ,点D是BC的中点,点E在AC上,且DE
,点D是BC的中点,点E在AC上,且DE
 E
E
(Ⅰ)证明:平面
 平面
平面 ;
;
(Ⅱ)求直线AD和平面 所成角的正弦值。
所成角的正弦值。

解法2 如图所示,设O是AC的中点,以O为原点建立空间直角坐标系,则相关各
点的坐标分别是A(2,0,0,),  .(2,0,
.(2,0,
 ),
D(-1,
),
D(-1, 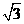 ), E(-1,0.0)
), E(-1,0.0)
易知 =(-3,
=(-3,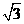 ,-
,- ),
), =(0,-
=(0,-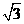 ,0),
,0),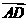 =(-3,
=(-3,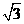 ,0)
,0)
设n=(x,y,z)是平面 DE的一个法向量,则
DE的一个法向量,则
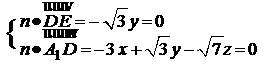

解得
故可取n=( ,0,-3,)于是
,0,-3,)于是

=
由此即知,直线AD和平面 DE所成的角是正弦为
DE所成的角是正弦为
18.(本小题满分12分)
如图4,在正三棱柱 中,
中,
D是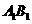 的中点,点E在
的中点,点E在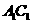 上,且
上,且 。
。
(I)
证明平面 平面
平面
(II)
求直线 和平面
和平面 所成角的正弦值。
所成角的正弦值。

解 (I)
如图所示,由正三棱柱 的性质知
的性质知 平面
平面
又DE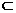 平面A
平面A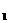 B
B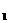 C
C ,所以DE
,所以DE AA
AA .
.
而DE AE。AA
AE。AA
 AE=A 所以DE
AE=A 所以DE 平面AC C
平面AC C A
A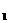 ,又DE
,又DE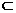 平面ADE,故平面ADE
平面ADE,故平面ADE 平面AC C
平面AC C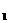 A
A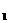 。
。
解法2 如图所示,设O使AC的中点,以O为原点建立空间直角坐标系,不妨设
A A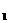 =
= ,则AB=2,相关各点的坐标分别是
,则AB=2,相关各点的坐标分别是
A(0,-1,0), B(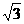 ,0,0), C
,0,0), C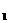 (0,1,
(0,1, ), D(
), D( ,-
,- ,
, )。
)。
易知 =(
=(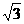 ,1,0),
,1,0),  =(0,2,
=(0,2, ),
), 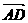 =(
=( ,-
,- ,
, )
)
设平面ABC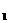 的法向量为n=(x,y,z),则有
的法向量为n=(x,y,z),则有


解得x=- y, z=-
y, z=- ,
,
故可取n=(1,-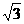 ,
, )。
)。
所以, (n·
(n·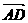 )=
)= =
= =
=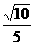 。
。
由此即知,直线AD和平面AB C 所成角的正弦值为
所成角的正弦值为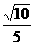 。
。
10. (本小题满分13分,(Ⅰ)小问7分,(Ⅱ)小问6分)
(本小题满分13分,(Ⅰ)小问7分,(Ⅱ)小问6分)
如题(18)图,在五面体ABCDEF中,AB//DC,∠BAD= ,CD=AD=2.,四边形ABFE为平行四边形,FA⊥平面ABCD,FC=3,ED=
,CD=AD=2.,四边形ABFE为平行四边形,FA⊥平面ABCD,FC=3,ED= ,求:
,求:
(Ⅰ)直线AB到平面EFCD的距离:
(Ⅱ)二面角F-AD-E的平面角的正切值,
9.(本小题共14分)
 如图,四棱锥
如图,四棱锥 的底面是正方形,
的底面是正方形, ,点E在棱PB上.
,点E在棱PB上.
(Ⅰ)求证:平面 ;
;
(Ⅱ)当 且E为PB的中点时,求AE与
且E为PB的中点时,求AE与
平面PDB所成的角的大小.
[解法2]如图,以D为原点建立空间直角坐标系 ,
,
设
则 ,
,
(Ⅰ)∵ ,
,
∴ ,
,
∴AC⊥DP,AC⊥DB,∴AC⊥平面PDB,
∴平面 .
.
(Ⅱ)当 且E为PB的中点时,
且E为PB的中点时, ,
,
设AC∩BD=O,连接OE,
由(Ⅰ)知AC⊥平面PDB于O,
∴∠AEO为AE与平面PDB所的角,
∵ ,
,
∴ ,
,
∴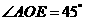 ,即AE与平面PDB所成的角的大小为
,即AE与平面PDB所成的角的大小为 .
.
19. (本小题满分12分,(Ⅰ)问5分,(Ⅱ)问7分)
(本小题满分12分,(Ⅰ)问5分,(Ⅱ)问7分)
如题(19)图,在四棱锥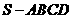 中,
中,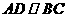 且
且 ;平面
;平面
 平面
平面 ,
, ;
; 为
为 的中点,
的中点,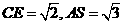 .求:
.求:
(Ⅰ)点 到平面
到平面 的距离;
的距离;
(Ⅱ)二面角 的大小.
的大小.
(Ⅰ)如答(19)图2,以S(O)为坐标原点,射线OD,OC分别为x轴,y轴正向,建立空间坐标系,设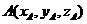 ,因平面
,因平面
即点A在xoz平面上,因此
又

因AD//BC,故BC⊥平面CSD,即BCS与平面
yOx重合,从而点A到平面BCS的距离为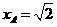 .
.
(Ⅱ)易知C(0,2,0),D(,0,0). 因E为BS的中点.
ΔBCS为直角三角形 ,
知 
设B(0,2,  ),
), >0,则
>0,则 =2,故B(0,2,2),所以E(0,1,1) .
=2,故B(0,2,2),所以E(0,1,1) .
在CD上取点G,设G(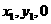 ),使GE⊥CD .
),使GE⊥CD .
由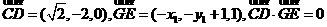 故
故
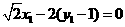 ①
①
又点G在直线CD上,即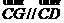 ,由
,由 =(
=( ),则有
),则有 ②
②
联立①、②,解得G= ,
,
故 =
=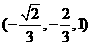 .又由AD⊥CD,所以二面角E-CD-A的平面角为向量
.又由AD⊥CD,所以二面角E-CD-A的平面角为向量 与向量
与向量 所成的角,记此角为
所成的角,记此角为 .
.
因为 =
= ,
,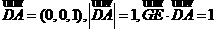 ,所以
,所以

故所求的二面角的大小为  .
.
 作
作 于
于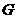 ,连
,连 ,则
,则 ,
, 为二面角
为二面角 的平面角,
的平面角,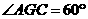 .不妨设
.不妨设 ,则
,则 .在
.在 中,由
中,由 ,易得
,易得 .
.
设点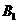 到面
到面 的距离为
的距离为 ,
,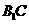 与平面
与平面 所成的角为
所成的角为 。利用
。利用 ,可求得
,可求得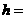
 ,又可求得
,又可求得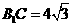

即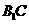 与平面
与平面 所成的角为
所成的角为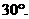
分析二:作出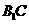 与平面
与平面 所成的角再行求解。如图可证得
所成的角再行求解。如图可证得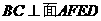 ,所以面
,所以面 。由分析一易知:四边形
。由分析一易知:四边形 为正方形,连
为正方形,连 ,并设交点为
,并设交点为 ,则
,则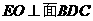 ,
, 为
为 在面
在面 内的射影。
内的射影。 。以下略。
。以下略。
分析三:利用空间向量的方法求出面 的法向量
的法向量 ,则
,则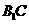 与平面
与平面 所成的角即为
所成的角即为 与法向量
与法向量 的夹角的余角。具体解法详见高考试题参考答案。
的夹角的余角。具体解法详见高考试题参考答案。
总之在目前,立体几何中的两种主要的处理方法:传统方法与向量的方法仍处于各自半壁江山的状况。命题人在这里一定会兼顾双方的利益。
8.(本小题满分12分)
如图,直三棱柱 中,
中, 、
、 分别为
分别为 、
、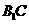 的中点,
的中点, 平面
平面
(I)证明:
(II)设二面角 为60°,求
为60°,求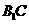 与平面
与平面 所成的角的大小。
所成的角的大小。
分析一:求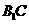 与平面
与平面 所成的线面角,只需求点
所成的线面角,只需求点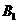 到面
到面 的距离即可。
的距离即可。
17.解析:(1)在如图,以D为坐标原点,建立空间直角坐标
依题意,得 。
。


 ,
,
所以异面直线 与
与 所成角的余弦值为
所成角的余弦值为 .A
.A
(2)假设在线段 上存在点
上存在点 ,使得
,使得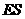
 平面
平面 .
.
 ,
,
可设
又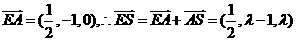 .
.
由 平面
平面 ,得
,得 即
即
故 ,此时
,此时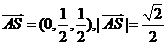 .
.
经检验,当 时,
时, 平面
平面 .
.
故线段 上存在点
上存在点 ,使得
,使得 平面
平面 ,此时
,此时 .
.
7.(13分)
 如图,四边形ABCD是边长为1的正方形,
如图,四边形ABCD是边长为1的正方形, ,
,
 ,且MD=NB=1,E为BC的中点
,且MD=NB=1,E为BC的中点
(1) 求异面直线NE与AM所成角的余弦值
(2)
在线段AN上是否存在点S,使得ES 平面AMN?若存在,求线段AS的长;若不存在,请说明理由
平面AMN?若存在,求线段AS的长;若不存在,请说明理由
6.(本小题满分12分)
如图,已知两个正方行ABCD 和DCEF不在同一平面内,M,N分别为AB,DF的中点 。
(I)若平面ABCD ⊥平面DCEF,求直线MN与平面DCEF所成角的正值弦;
(II)用反证法证明:直线ME 与 BN 是两条异面直线。

设正方形ABCD,DCEF的边长为2,以D为坐标原点,分别以射线DC,DF,DA为x,y,z轴正半轴建立空间直角坐标系如图.
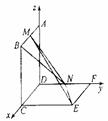 则M(1,0,2),N(0,1,0),可得
则M(1,0,2),N(0,1,0),可得 =(-1,1,2).
=(-1,1,2).
又 =(0,0,2)为平面DCEF的法向量,
=(0,0,2)为平面DCEF的法向量,
可得cos( ,
,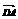 )=
)= ·
·
所以MN与平面DCEF所成角的正弦值为
cos ·
……6分
·
……6分
(Ⅱ)假设直线ME与BN共面, ……8分
则AB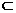 平面MBEN,且平面MBEN与平面DCEF交于EN
平面MBEN,且平面MBEN与平面DCEF交于EN
由已知,两正方形不共面,故AB 平面DCEF。
平面DCEF。
又AB//CD,所以AB//平面DCEF。面EN为平面MBEN与平面DCEF的交线,
所以AB//EN。
又AB//CD//EF,
所以EN//EF,这与EN∩EF=E矛盾,故假设不成立。
所以ME与BN不共面,它们是异面直线. ……12分
3.(本小题满分12分)
 如图,在五面体ABCDEF中,FA
如图,在五面体ABCDEF中,FA  平面ABCD, AD//BC//FE,AB
平面ABCD, AD//BC//FE,AB AD,M为EC的中点,AF=AB=BC=FE=
AD,M为EC的中点,AF=AB=BC=FE= AD
AD
(I) 求异面直线BF与DE所成的角的大小;
(II)
证明平面AMD 平面CDE;
平面CDE;
(III)求二面角A-CD-E的余弦值。
如图所示,建立空间直角坐标系,
点 为坐标原点。设
为坐标原点。设 依题意得
依题意得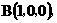
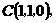


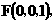

(I)


所以异面直线 与
与 所成的角的大小为
所成的角的大小为 .
.
(II)证明:
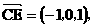
 ,
,

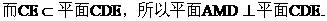
(III)

又由题设,平面 的一个法向量为
的一个法向量为


|
 平面
平面 ,
,
是以 为斜边的等腰直角三角形,
为斜边的等腰直角三角形, 分别为
分别为 ,
,
 ,
, 的中点,
的中点, ,
,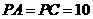 .
.
(I)设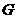 是
是 的中点,证明:
的中点,证明: 平面
平面 ;
;
(II)证明:在 内存在一点
内存在一点 ,使
,使 平面
平面 ,并求点
,并求点 到
到 ,
, 的距离.
的距离.
证明:(I)如图,连结OP,以O为坐标原点,分别以OB、OC、OP所在直线为 轴,
轴, 轴,
轴, 轴,建立空间直角坐标系O
轴,建立空间直角坐标系O ,
,
则
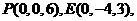
 ,由题意得,
,由题意得,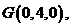 因
因 ,因此平面BOE的法向量为
,因此平面BOE的法向量为 ,
, 得
得 ,又直线
,又直线 不在平面
不在平面 内,因此有
内,因此有 平面
平面
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com