10.(2010湖北理)14．某射手射击所得环数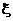的分布列如下：

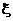	7	8	9	10
P	x	0.1	0.3	y

已知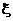的期望E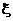=8.9，则y的值为　　　 .

[答案]0.4

[解析]由表格可知：

联合解得.

9.(2010安徽理)15、甲罐中有5个红球，2个白球和3个黑球，乙罐中有4个红球，3个白球和3个黑球。先从甲罐中随机取出一球放入乙罐，分别以和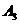表示由甲罐取出的球是红球，白球和黑球的事件；再从乙罐中随机取出一球，以表示由乙罐取出的球是红球的事件，则下列结论中正确的是________(写出所有正确结论的编号)。

①；　 ②；　 ③事件与事件相互独立；

④是两两互斥的事件；　 ⑤的值不能确定，因为它与中哪一个发生有关

[答案]②④

[解析]易见是两两互斥的事件，而

。

[方法总结]本题是概率的综合问题，掌握基本概念，及条件概率的基本运算是解决问题的关键.本题在是两两互斥的事件，把事件B的概率进行转化，可知事件B的概率是确定的.

8.(2010湖南理)9．已知一种材料的最佳入量在110g到210g之间。若用0.618法安排实验，则第一次试点的加入量可以是　　　　　　　　 g

7.(2010湖南理)11．在区间上随机取一个数x，则的概率为　　　

6.(2010湖北文)13.一个病人服用某种新药后被治愈的概率为0.9.则服用这咱新药的4个病人中至少3人被治愈的概率为_______(用数字作答)。

[答案]0.9744

[解析]分情况讨论:若共有3人被治愈，则；

若共有4人被治愈，则，故至少有3人被治愈概率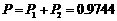

5.(2010重庆理)(13)某篮球队员在比赛中每次罚球的命中率相同，且在两次罚球中至多命中一次的概率为，则该队员每次罚球的命中率为____________.

解析：由得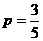

4.(2010重庆文)(14)加工某一零件需经过三道工序，设第一、二、三道工序的次品率分别为、、，且各道工序互不影响，则加工出来的零件的次品率为____________ .

解析：加工出来的零件的次品的对立事件为零件是正品，由对立事件公式得

加工出来的零件的次品率

3.(2010辽宁文)(13)三张卡片上分别写上字母E、E、B，将三张卡片随机地排成一行，

恰好排成英文单词BEE的概率为　　　　　 。　

[答案]

解析： 题中三张卡片随机地排成一行，共有三种情况：，

概率为：

2.(2010湖南文)11.在区间[-1,2]上随即取一个数x，则x∈[0,1]的概率为　　　　　　　 。

[答案]

[命题意图]本题考察几何概率，属容易题。

1.(2010上海文)10. 从一副混合后的扑克牌(52张)中随机抽取2张，则“抽出的2张

均为红桃”的概率为　　　　　　 (结果用最简分数表示)。

[答案]

解析：考查等可能事件概率“抽出的2张均为红桃”的概率为