
题目列表(包括答案和解析)
10.设数列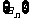 的前n项和Sn,且
的前n项和Sn,且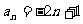 ,则数列
,则数列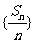 的前11项为( )
的前11项为( )
A.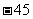 B.
B.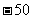 C.
C.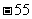 D.
D.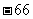
9.设等比数列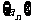 的首相为
的首相为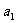 ,公比为q ,则“
,公比为q ,则“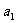 < 0 且0< q <1”是“对于任意
< 0 且0< q <1”是“对于任意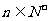 都有
都有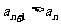 ”的 ( )
”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充分比要条件 D.既不充分又不必要条件
8.将自然数0,1,2,…按照如下形式进行排列:
 ,
,
根据以上规律判定,从2007到2009的箭头方向是( )
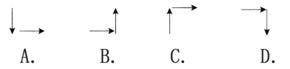
7.设等比数列{an}的前n项和为Sn,若S10:S5=1:2,则S15:S5=( ) A.3:4 B.2:3 C.1:2 D.1:3
5.已知数列{an}是等比数列,且每一项都是正数,若a2,a48是2x2-7x+6=0的两个根,则 a1·a2·a25·a48·a49的值为( )
A.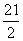 B.9
B.9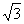 C.±9
C.±9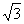 D.35
6.等差数列
D.35
6.等差数列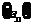 中,已知
中,已知 ,那么
,那么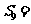 ( )
( )
A.2; B.8; C.18; D.36
4.已知等差数列{an}的前2006项的和S2006=2008,其中所有的偶数项的和是2,则a1003的值为( )
A.1 B.2 C.3 D.4
3.如果数列{an}满足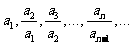 是首项为1,公比为2的等比数列,则a100等于( )
是首项为1,公比为2的等比数列,则a100等于( )
A.2100 B.299 C.25050 D.24950
2.已知数列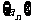 的前n项和为
的前n项和为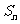 ,且
,且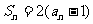 , 则
, 则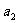 等于( )
等于( )
A.4 B.2 C.1 D.-2
1.集合A={1,2,3,4,5,6},从集合A中任选3个不同的元素组成等差数列,这样的等差数列共有( )
A.4个 B.8个 C.10个 D.12个
2.利率问题:①单利问题:如零存整取储蓄(单利)本利和计算模型:若每期存入本金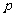 元,每期利率为
元,每期利率为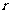 ,则
,则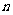 期后本利和为:
期后本利和为: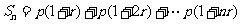
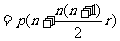 (等差数列问题);②复利问题:按揭贷款的分期等额还款(复利)模型:若贷款(向银行借款)
(等差数列问题);②复利问题:按揭贷款的分期等额还款(复利)模型:若贷款(向银行借款)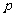 元,采用分期等额还款方式,从借款日算起,一期(如一年)后为第一次还款日,如此下去,分
元,采用分期等额还款方式,从借款日算起,一期(如一年)后为第一次还款日,如此下去,分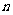 期还清。如果每期利率为
期还清。如果每期利率为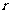 (按复利),那么每期等额还款
(按复利),那么每期等额还款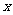 元应满足:
元应满足: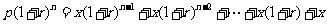 (等比数列问题)。
(等比数列问题)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com