
题目列表(包括答案和解析)
(15) 设数列{an}的首项a1=a≠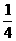 ,且
,且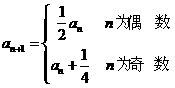 ,
,
记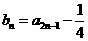 ,n==l,2,3,…·.
,n==l,2,3,…·.
(I)求a2,a3;
(II)判断数列{bn}是否为等比数列,并证明你的结论;
(III)求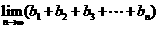
(16) 数列{an}的前n项和为Sn,且a1=1,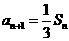 ,n=1,2,3,……,求
,n=1,2,3,……,求
(I)a2,a3,a4的值及数列{an}的通项公式;
(II)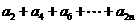 的值.
的值.
(17) 已知{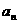 }是公比为q的等比数列,且
}是公比为q的等比数列,且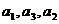 成等差数列.
成等差数列.
(Ⅰ)求q的值;
(Ⅱ)设{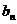 }是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
}是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
.
(18) 已知定义在R上的函数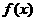 和数列
和数列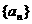 满足下列条件:
满足下列条件:
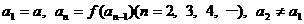 ,
,
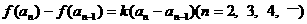 ,其中a为常数,k为非零常数.
,其中a为常数,k为非零常数.
(Ⅰ)令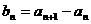
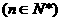 ,证明数列
,证明数列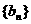 是等比数列;
是等比数列;
(Ⅱ)求数列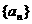 的通项公式;
的通项公式;
(Ⅲ)当 时,求
时,求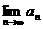 .
.
(11) 在等差数列{an}中,a1>0,a5=3a7,前n项和为Sn,若Sn取得最大值,则n= .
(12) 在等差数列{an}中,前n项和为Sn,若S19=31,S31=19,则S50的值是______
(13)在等比数列{an}中,若a9·a11=4,则数列{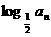 }前19项之和为_______
}前19项之和为_______
(14)若a>0,且a≠1, 则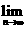
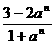 的值是
.
的值是
.
(1) 已知等差数列{an}的前n项和为Sn,且S4=3,S8=7,则S12的值是 ( )
A 8 B 11 C 12 D 15
(2) 已知数列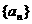 满足
满足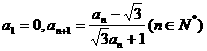 ,则
,则 = ( )
= ( )
A 0 B 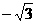 C
C 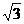 D
D 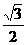
(3) 数列1,(1+2),(1+2+22),…,( 1+2+22+…+2n-1+…)的前n项和是 ( )
A 2n B 2n-2 C 2n+1- n -2 D n·2n
(4) 从集合{1,2,3,4,5,6,7,8,9,10}中任选三个不同的数,如果这三个数经过适当的排列成等差数列,则这样的等差数列一共有 ( )
A 20个 B 40个 C 10个 D 120个
(5) 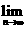
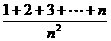 =
( )
=
( )
A 2
B 4 C 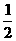 D
0
D
0
(6) 如果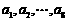 为各项都大于零的等差数列,公差
为各项都大于零的等差数列,公差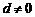 ,则
( )
,则
( )
A 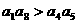 B
B 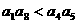 C
C 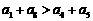 D
D 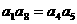
(7)已知等差数列{an}与{bn}的前n项和分别为Sn与Tn, 若 , 则
, 则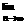
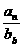 的值是
( )
的值是
( )
A 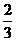 B
B 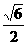 C
C 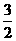 D
D 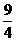
(8) 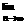
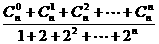 的值是
(
)
的值是
(
)
A 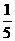 B
B
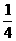 C
C
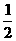 D
D 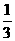
(9) 已知数列{log2(an-1)}(n∈N*)为等差数列,且a1=3,a2=5,则
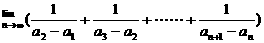 =
(
)
=
(
)
A 2 B 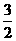 C 1 D
C 1 D 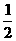
(10) 已知数列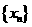 满足
满足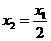 ,
,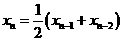 ,
,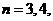 ….若
….若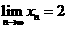 ,则 ( )
,则 ( )
A 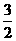 B3
C4
D5
B3
C4
D5
(15) 已知向量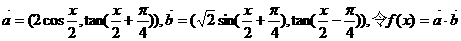 .
.
是否存在实数 若存在,则求出x的值;若不存在,则证明之.
若存在,则求出x的值;若不存在,则证明之.
(16)如图,在Rt△ABC中,已知BC=a,若长为2a的线段PQ以点A为中点,问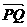
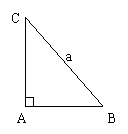 与
与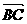 的夹角θ取何值时,
的夹角θ取何值时,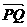 ·
·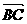 的值最大?并求出这个最大值.
的值最大?并求出这个最大值.
(17)已知两点M(-1,0), N(1, 0), 且点P使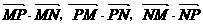 成公差小于零的等差数列.
成公差小于零的等差数列.
(Ⅰ)点P的轨迹是什么曲线?
(Ⅱ)若点P的坐标为(x0, y0),
记θ为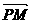 ,
,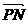 的夹角, 求tanθ.
的夹角, 求tanθ.
(18) 中,内角
中,内角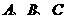 的对边分别是
的对边分别是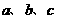 ,已知
,已知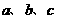 成等比数列,且
成等比数列,且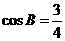
(Ⅰ)求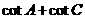 的值
的值
(Ⅱ)设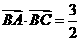 ,求
,求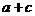 的值。
的值。
(11)已知向量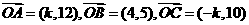 ,且A、B、C三点共线,则k=___
,且A、B、C三点共线,则k=___
(12)已知向量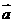 与
与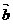 的夹角为120°,且|
的夹角为120°,且|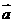 |=2, |
|=2, |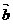 |=5,则(2
|=5,则(2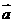 -
-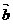 )·
)·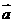 =
.
=
.
(13已知向量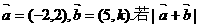 不超过5,则k的取值范围是_______
不超过5,则k的取值范围是_______
(14) 直角坐标平面 中,若定点
中,若定点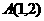 与动点
与动点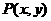 满足
满足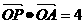 ,则点P的轨迹方程是__________
,则点P的轨迹方程是__________
(1) 若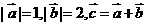 ,且
,且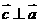 ,则向量
,则向量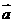 与
与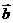 的夹角为
(
)
的夹角为
(
)
A 30° B 60° C 120° D 150°
(2) P是△ABC所在平面上一点,若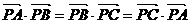 ,则P是△ABC的( )
,则P是△ABC的( )
A 外心 B 内心 C 重心 D 垂心
(3)已知平行四边形ABCD中, 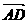 =(3, 7 ),
=(3, 7 ), 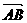 =(-2, 3 ), 对角线AC, BD交于点O,
=(-2, 3 ), 对角线AC, BD交于点O,
则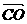 的坐标为
(
)
的坐标为
(
)
A (-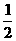 , 5) B
(-
, 5) B
(-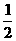 , -5)
C
(
, -5)
C
(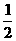 , -5) D (
, -5) D (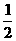 , 5)
, 5)
(4) 已知向量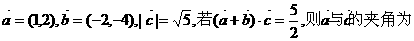 ( )
( )
A 30° B 60° C 120° D 150°
(5)为了得到函数y=sin(2x-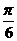 )的图像,可以将函数y=cos2x的图像
( )
)的图像,可以将函数y=cos2x的图像
( )
A 向右平移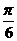 个单位长度
B 向右平移
个单位长度
B 向右平移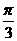 个单位长度
个单位长度
C 向左平移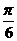 个单位长度
D 向左平移
个单位长度
D 向左平移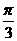 个单位长度
个单位长度
(6) 点P在平面上作匀速直线运动,速度向量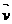 =(4,-3)(即点P的运动方向与v相同,且每秒移动的距离为|
=(4,-3)(即点P的运动方向与v相同,且每秒移动的距离为|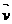 |个单位.设开始时点P的坐标为(-10,10),则5秒后点P的坐标为
( )
|个单位.设开始时点P的坐标为(-10,10),则5秒后点P的坐标为
( )
A (-2,4) B (-30,25) C (10,-5) D (5,-10)
(7) 在△ABC中,∠C=90°,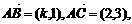 则k的值是 ( )
则k的值是 ( )
A 5 B -5 C 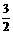 D
D 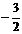
(8) 已知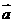 、
、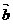 均为单位何量,它们的夹角为60°,那么|
均为单位何量,它们的夹角为60°,那么| 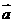 + 3
+ 3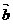 | =
(
)
| =
(
)
A 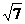 B
B 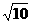 C
C 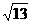 D 4
D 4
(9) 已知点A(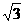 ,1),B(0,0)C(
,1),B(0,0)C(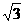 ,0).设∠BAC的平分线AE与BC相交于E,那么有
,0).设∠BAC的平分线AE与BC相交于E,那么有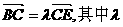 等于
( )
等于
( )
A 2
B 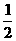 C -3
D -
C -3
D -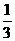
(10)
已知向量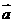 ≠
≠ ,|
,| |=1,对任意t∈R,恒有|
|=1,对任意t∈R,恒有|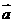 -t
-t |≥|
|≥|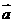 -
- |,则
( )
|,则
( )
A 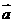 ⊥
⊥ B
B
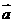 ⊥(
⊥(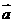 -
- ) C
) C  ⊥(
⊥(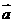 -
- ) D (
) D (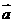 +
+ )⊥(
)⊥(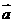 -
- )
)
(15) 已知 ,
,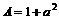 ,
,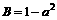 ,
,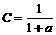 ,试比较A、B、C的大小.
,试比较A、B、C的大小.
(16) 已知正数x、y满足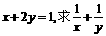 的最小值.
的最小值.
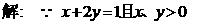
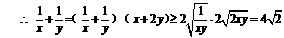
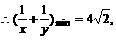
判断以上解法是否正确?说明理由;若不正确,请给出正确解法.
(17) 已知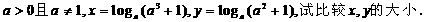
(18) 已知函数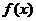 在R上是增函数,
在R上是增函数,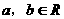 .
.
(1)求证:如果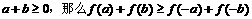 ;
;
(2)判断(1)中的命题的逆命题是否成立?并证明你的结论;
解不等式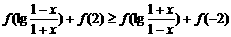 .
.
(11) 设a<0,-1<b<0,则a,ab,ab2从小到大的顺序为__________
(12) 设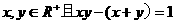 ,则x+y的最小值为_________
,则x+y的最小值为_________
(13)若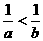 <0,已知下列不等式:①a+b<ab ②|a|>|b| ③a<b ④
<0,已知下列不等式:①a+b<ab ②|a|>|b| ③a<b ④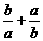 >2,
>2,
其中正确的不等式的序号为 .
(14)设集合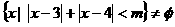 ,则m的取值范围是 .
,则m的取值范围是 .
(1) 已知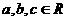 ,那么下列命题中正确的是 ( )
,那么下列命题中正确的是 ( )
A.若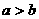 ,则
,则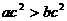 B.若
B.若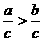 ,则
,则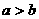
C.若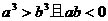 ,则
,则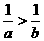 D.若
D.若 ,则
,则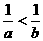
(2) 设a>1,0<b<1,则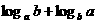 的取值范围为 ( )
的取值范围为 ( )
A.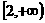 B.
B.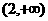 C.
C.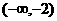 D.
D.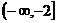
(3) 设x>0,P=2x+2-x,Q=(sinx+cosx)2,则 ( )
A.P≥Q B.P≤Q C.P>Q D.P<Q
(4)命题p:若a、b∈R,则|a|+|b|>1是|a+b|>1的充分而不必要条件.
命题q:函数y=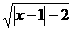 的定义域是(-∞,-1
的定义域是(-∞,-1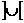 3,+∞).则 ( )
3,+∞).则 ( )
A . “p或q”为假 B. “p且q”为真 C. p真q假 D . p假q真
(5)如果a,b,c满足c<b<a,且ac<0,那么下列选项中不一定成立的是 ( )
A. ab>ac B. c(b-a)>0 C. cb2<ab2 D. ac(a-c)<0
(6)若a、b为实数, 且a+b=2, 则3a+3b的最小值为 ( )
A .18 B .6 C .2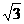 D .2
D .2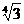
(7) 设p+q=1, p>0, q>0, 则不等式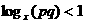 成立的一个充分条件是
( )
成立的一个充分条件是
( )
A .
0<x< B .
B . <x<
<x<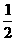 C .
C .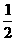 <x<1 D. x>1
<x<1 D. x>1
(8) 设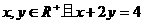 ,则
,则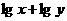 的最大值是 ( )
的最大值是 ( )
A.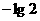 B.
B. C.
C.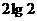 D.2
D.2
(9) 设a>0, b>0,则以下不等式中不恒成立的是 ( )
A.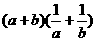 ≥4
B.
≥4
B.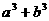 ≥
≥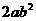
C.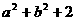 ≥
≥ D.
D.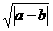 ≥
≥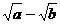
(10) 设0<x<1,a、b为正常数,则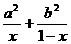 的最小值为 ( )
的最小值为 ( )
A.4ab B.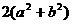 C.
C.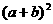 D.
D.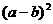
22.(本小题满分12分)某厂家拟在2010年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)x万件与年促销费用m万元(m≥0)满足x=3-(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2010年该产品的利润y万元表示为年促销费用m万元的函数;
(2)该厂家2010年的促销费用投入多少万元时,厂家的利润最大.
解析:(1)由题意可知当m=0时,x=1(万件),
∴1=3-k⇒k=2.∴x=3-.
每件产品的销售价格为1.5×(元),
∴2010年的利润y=x·(1.5×)-(8+16x+m)
=4+8x-m=4+8(3-)-m
=-[+(m+1)]+29(m≥0).
(2)∵m≥0时,+(m+1)≥2=8,
∴y≤-8+29=21,当且仅当=m+1⇒m=3(万元)时,ymax=21(万元).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com