
题目列表(包括答案和解析)
17.P为直径AB=4的半圆上一点,C为AB延长线上一点,BC=2,△PCQ为正△,问
∠POC为多大时,四边形OCQP面积最大,最大面积为多少?
16.求 的最小正周期、最大值、最小值
的最小正周期、最大值、最小值
(11)把函数y = cos(x+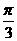 )的图象向左平移m个单位(m>0), 所得图象关于y轴对称, 则m的最小值是_________。
)的图象向左平移m个单位(m>0), 所得图象关于y轴对称, 则m的最小值是_________。
(12)函数y = -2sin(4x+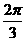 )的图象与x轴的交点中, 离原点最近的一点的坐标是_______。
)的图象与x轴的交点中, 离原点最近的一点的坐标是_______。
(13)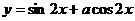 的图象关于
的图象关于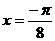 对称,则a等于___________。
对称,则a等于___________。
(14)①存在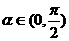 使
使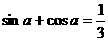
②存在区间(a,b)使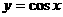 为减函数而
为减函数而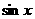 <0
<0
③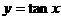 在其定义域内为增函数
在其定义域内为增函数
④ 既有最大、最小值,又是偶函数
既有最大、最小值,又是偶函数
⑤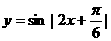 最小正周期为π
最小正周期为π
以上命题错误的为____________。
三解答题:
15.函数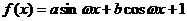 最小正周期为π,最大值为3,且
最小正周期为π,最大值为3,且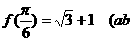 ≠0),求f (x)的的解析式。
≠0),求f (x)的的解析式。
(1)下列函数中,最小正周期为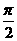 的是
( )
的是
( )
A.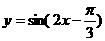 B.
B.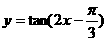
C.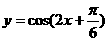 D.
D.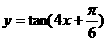
(2)将函数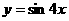 的图象向左平移
的图象向左平移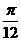 个单位,得到
个单位,得到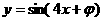 的图象,则
的图象,则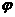 等于
( )
等于
( )
A.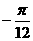 B.
B.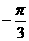 C.
C.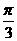 D.
D.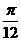
(3)下列命题中正确的是 ( )
A.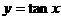 为增函数 B.
为增函数 B.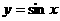 在第一象限为增函数
在第一象限为增函数
C.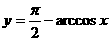 为奇函数 D.
为奇函数 D.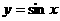 的反函数为
的反函数为
(4) 单调增区间为
( )
单调增区间为
( )
A.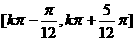 B.
B.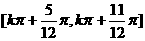
C. D.
D.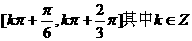
(5)函数y = - xcosx的部分图象是 ( )
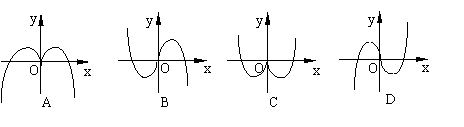 (6)
(6)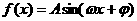 (A>0,ω>0)在x=1处取最大值,则
( )
(A>0,ω>0)在x=1处取最大值,则
( )
A.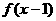 一定是奇函数 B.
一定是奇函数 B.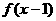 一定是偶函数
一定是偶函数
C.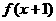 一定是奇函数 D.
一定是奇函数 D.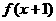 一定是偶函数
一定是偶函数
(7)已知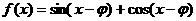 为奇函数,则
为奇函数,则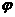 的一个取值
( )
的一个取值
( )
A.0
B.π C.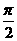 D.
D.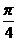
(8)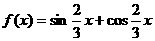 的图象中相邻的两条对称轴间距离为
( )
的图象中相邻的两条对称轴间距离为
( )
A.3π
B.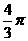 C.
C.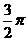 D.
D.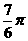
(9)函数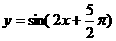 的一条对称轴方程(
)
的一条对称轴方程(
)
A.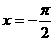 B.
B.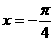 C.
C.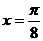 D.
D.

(10)使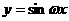 (ω>0)在区间[0,1]至少出现2次最大值,则ω的最小值为( )
(ω>0)在区间[0,1]至少出现2次最大值,则ω的最小值为( )
A.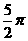 B.
B. C.π D.
C.π D.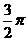
(15) 已知sin(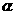 +
+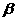 )=-
)=-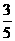 ,cos(
,cos(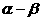 )=
)=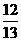 ,且
,且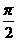 <
<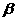 <
<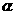 <
<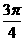 ,求sin2
,求sin2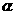 .
.
(16) (已知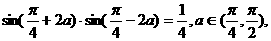
求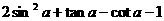 的值.
的值.
(17) 在△ABC中,sinA+cosA=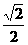 ,AC=2,AB=3,求tgA的值和△ABC的面积.
,AC=2,AB=3,求tgA的值和△ABC的面积.
(18)设关于x的方程sinx+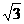 cosx+a=0在(0, 2π)内有相异二解α、β.
cosx+a=0在(0, 2π)内有相异二解α、β.
(11)若tan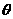 =2,则2sin2
=2,则2sin2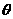 -3sin
-3sin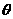 cos
cos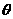 = 。
= 。
(12)若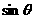 -
-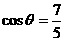 ,
,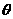 ∈(0,π),则tan
∈(0,π),则tan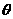 =
。
=
。
(13) ,则
,则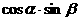 范围
。
范围
。
(14)下列命题正确的有_________。
①若-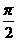 <
<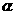 <
<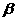 <
<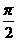 ,则
,则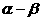 范围为(-π,π);
范围为(-π,π);
②若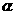 在第一象限,则
在第一象限,则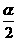 在一、三象限;
在一、三象限;
③若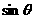 =
=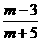 ,
,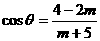 ,则m∈(3,9);
,则m∈(3,9);
④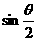 =
=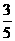 ,
, =
=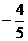 ,则
,则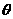 在一象限。
在一象限。
(1)
若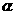 为第三象限,则
为第三象限,则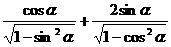 的值为
( )
的值为
( )
A.3 B.-3 C.1 D.-1
(2) 以下各式中能成立的是 ( )
A. B.
B.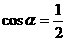 且
且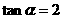
C.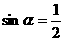 且
且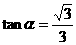 D.
D.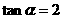 且
且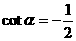
(3) sin7°cos37°-sin83°cos53°值 ( )
A. B.
B.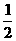 C.
C.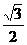 D.-
D.-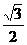
(4)若函数f(x)=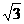 sin
sin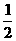 x, x∈[0,
x, x∈[0, 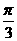 ], 则函数f(x)的最大值是
(
)
], 则函数f(x)的最大值是
(
)
A 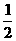 B
B
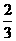 C
C
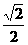 D
D
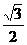
(5)
条件甲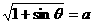 ,条件乙
,条件乙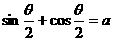 ,那么
( )
,那么
( )
A.甲是乙的充分不必要条件 B.甲是乙的充要条件
C.甲是乙的必要不充分条件 D.甲是乙的既不充分也不必要条件
(6)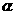 、
、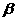 为锐角a=sin(
为锐角a=sin(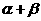 ),b=
),b=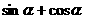 ,则a、b之间关系为 ( )
,则a、b之间关系为 ( )
A.a>b B.b>a C.a=b D.不确定
(7)(1+tan25°)(1+tan20°)的值是 ( )
A -2 B 2 C 1 D -1
(8)
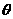 为第二象限的角,则必有
( )
为第二象限的角,则必有
( )
A.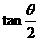 >
>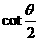 B.
B.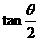 <
<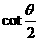
C.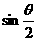 >
> D.
D.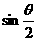 <
<
(9)在△ABC中,sinA=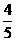 ,cosB=
,cosB=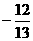 ,则cosC等于
( )
,则cosC等于
( )
A.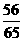 B.
B.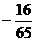 C.
C.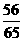 或
或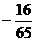 D.
D.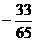
(10) 若a>b>1, P=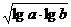 , Q=
, Q=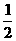 (lga+lgb),R=lg
(lga+lgb),R=lg  , 则
( )
, 则
( )
A.R<P<Q B.P<Q<R C.Q<P<R D P<R<Q
(15) 已知数列 为等差数列,且
为等差数列,且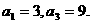 求数列
求数列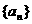 的通项公式;
的通项公式;
(16) 设数列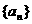 的前n项和为Sn=2n2,
的前n项和为Sn=2n2, 为等比数列,且
为等比数列,且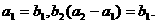
(Ⅰ)求数列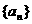 和
和 的通项公式;
的通项公式;
(Ⅱ)设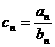 ,求数列
,求数列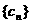 的前n项和Tn.
的前n项和Tn.
(17) 已知等比数列{an}的各项都是正数, Sn=80, S2n=6560, 且在前n项中, 最大的项为54, 求n的值.
(18) 已知{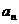 }是公比为q的等比数列,且
}是公比为q的等比数列,且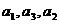 成等差数列.
成等差数列.
(Ⅰ)求q的值;
(Ⅱ)设{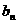 }是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由..
}是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由..
(11) 在 和
和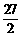 之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积为_____.
之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积为_____.
(12) 设数列{an}的前n项和为Sn,Sn=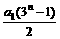 (对于所有n≥1),且a4=54,则a1的数值是_____.
(对于所有n≥1),且a4=54,则a1的数值是_____.
(13) 等差数列{an}的前m项和为30, 前2m项和为100, 则它的前3m项和为 .
(14) 设等比数列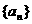 的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为_________
的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为_________
(1) 已知等差数列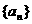 中,
中,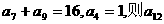 的值是 ( )
的值是 ( )
A 15 B 30 C 31 D 64
(2) 在各项都为正数的等比数列{an}中,首项a1=3 ,前三项和为21,则a3+ a4+ a5=( )
A 33 B 72 C 84 D 189
(3)已知等差数列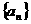 的公差为2,若
的公差为2,若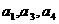 成等比数列, 则
成等比数列, 则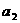 =
( )
=
( )
A –4 B –6 C –8 D –10
(4) 如果数列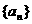 是等差数列,则
(
)
是等差数列,则
(
)
A 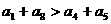 B
B
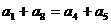
C 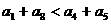 D
D
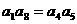
(5) 已知由正数组成的等比数列{an}中,公比q=2, a1·a2·a3·…·a30=245, 则
a1·a4·a7·…·a28= ( )
A 25 B 210 C 215 D 220
(6) 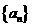 是首项
是首项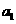 =1,公差为
=1,公差为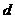 =3的等差数列,如果
=3的等差数列,如果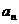 =2005,则序号
=2005,则序号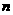 等于
( )
等于
( )
A 667 B 668 C 669 D 670
(7) 数列{an}的前n项和Sn=3n-c, 则c=1是数列{an}为等比数列的 ( )
A 充分非必要条件 B 必要非充分条件
C充分必要条件 D 既非充分又非必要条件
(8) 在等比数列{an}中, a1<0, 若对正整数n都有an<an+1, 那么公比q的取值范围是 ( )
A q>1 B 0<q<1 C q<0 D q<1
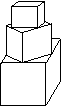
(9) 有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点。已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是 ( )
 A 4;
A 4;
B 5;
C 6;
D 7。
(10) 已知f(x)=bx+1为x的一次函数, b为不等于1的常数, 且
g(n)=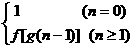 , 设an= g(n)-g(n-1) (n∈N※), 则数列{an}是
(
)
, 设an= g(n)-g(n-1) (n∈N※), 则数列{an}是
(
)
A 等差数列 B等比数列 C 递增数列 D 递减数列
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com