
题目列表(包括答案和解析)
21.(本小题满分12分)已知函数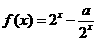 .
.
(1)将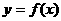 的图象向右平移两个单位,得到函数
的图象向右平移两个单位,得到函数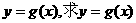 的解析式;
的解析式;
(2)函数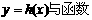
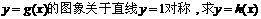 的解析式;
的解析式;
(3)设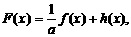
 的取值范围.
的取值范围.
20.(本小题满分12分) 求函数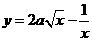 在
在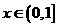 上的最大值,其中
上的最大值,其中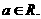
19.(本小题满分12分)设函数f(x)=ax2+8x+3 a<0
a<0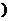 。对于给定的负数a,有一个最大的
。对于给定的负数a,有一个最大的
正数l(a),使得在整个区间[0,l(a)]上,不等式|f(x)|≤5恒成立.
问:a为何值时,l(a)最大?求出这个最大的l(a),证明你的结论.
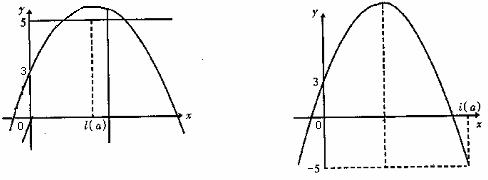
18.(本小题满分12分)设全集U=R
(1)解关于x的不等式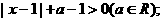
 (2)记A为(1)中不等式的解集,集合
(2)记A为(1)中不等式的解集,集合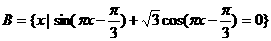 ,
,
若( ∪A)∩B恰有3个元素,求a的取值范围.
17.(本小题满分12分)已知数列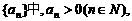 其前
其前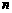 项和为
项和为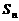 ,且
,且 ,当
,当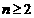 时,
时,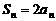 .
.
(1)求数列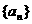 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列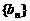 的前
的前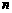 项和
项和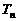 .
.
16.直线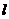 经过点
经过点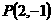 ,它在
,它在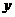 轴上的截距等于它在
轴上的截距等于它在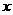 轴上截距的2倍,求直线
轴上截距的2倍,求直线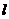 的方程。某学生作出了以下解答: 设直线
的方程。某学生作出了以下解答: 设直线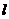 的方程为
的方程为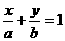 , 则
, 则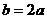 (1), ∵点
(1), ∵点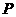 在直线
在直线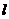 上,∴
上,∴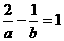 (2),解由(1)、(2)组成的方程组,得
(2),解由(1)、(2)组成的方程组,得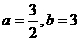 ,∴直线
,∴直线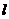 的方程为
的方程为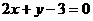 .
.
判断上述解法是否正确,如不正确,给出你的答案 .
15.从装有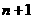 个球(其中
个球(其中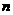 个白球,
个白球,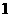 个黑球)的口袋中取出
个黑球)的口袋中取出 个球
个球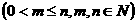 ,共有
,共有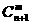 种取法。在这
种取法。在这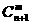 种取法中,可以分成两类:一类是取出的
种取法中,可以分成两类:一类是取出的 个球全部为白球,共有
个球全部为白球,共有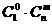 种取法;另一类是取出的
种取法;另一类是取出的 个球有
个球有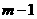 个白球和
个白球和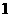 个黑球,共有
个黑球,共有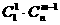 种取法。显然
种取法。显然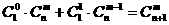 ,即有等式:
,即有等式: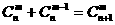 成立.试根据上述思想化简下列式子:
成立.试根据上述思想化简下列式子:
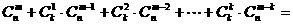
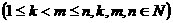 .
.
14.已知正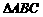 的边长为
的边长为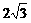 ,则到三个顶点的距离都为1的平面有_________个.
,则到三个顶点的距离都为1的平面有_________个.
13.定义符号函数
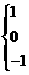
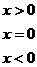 , 则不等式:
, 则不等式: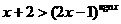 的解集是
.
的解集是
.
12.从5位男教师和4位女教师中选出3位教师,派到3个班担任班主任(每班1位班主任),要求这3位班主任中男、女教师都要有,则不同的选派方案共有 ( )
A.210种 B.420种 C.630种 D.840种
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com