
题目列表(包括答案和解析)
18. 已知圆
已知圆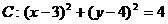 ,直线
,直线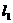 过定点
过定点 ;
;
 (1)若
(1)若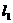 与圆相切,求
与圆相切,求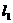 的方程;
的方程;
(2)若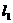 与圆相交于
与圆相交于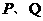 丙点,线段
丙点,线段 的中点为
的中点为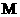 ,又
,又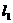 与
与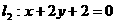 的交点为
的交点为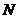 ,判断
,判断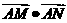 是否为定值,若是,则求出定值;若不是,请说明理由。
是否为定值,若是,则求出定值;若不是,请说明理由。
17.某货轮在A处看灯塔B在货轮北偏东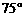 ,距离为
,距离为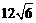 n mile;在A处看灯塔C在货轮的北偏西
n mile;在A处看灯塔C在货轮的北偏西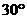 ,距离为
,距离为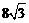 n mile.货轮由A处向正北航行到D处时,再看灯塔B在北偏东
n mile.货轮由A处向正北航行到D处时,再看灯塔B在北偏东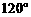 ,求:
,求:
(Ⅰ)A处与D处之间的距离;
(Ⅱ)灯塔C与D处之间的距离.
16.通过正三棱锥的底面一边且垂直于对棱作一截面,若此截面将对棱分成3:2两部分,且底面的边长为4,求棱锥的全面积.
15.△ABC中,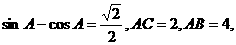 求角A的度数和△ABC的面积.(结果用数字表示,可保留根号)
求角A的度数和△ABC的面积.(结果用数字表示,可保留根号)
14.已知 ,且方程
,且方程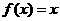 无实数根,下列命题:
无实数根,下列命题:
(1)方程 一定有实数根;
一定有实数根;
(2)若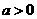 ,则不等式
,则不等式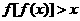 对一切实数
对一切实数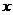 都成立;
都成立;
(3)若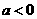 ,则必存在实数
,则必存在实数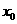 ,使
,使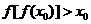
(4)若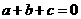 ,则不等式
,则不等式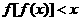 对一切实数
对一切实数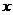 都成立.
都成立.
其中,正确命题的序号是____________.(把你认为正确的命题的所有序号都填上)
13.在△ABC中,AB=2,AC=1,D为BC的中点,则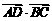 =_________.
=_________.
12.定义“和常数列”:在一个数列中,如果每一项与它的后一项和都为同一个常数,那么这个数列叫做常数列,这个常数叫做该数列的和常;已知数列{an}是和常数列,且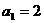 ,和常为5,那么
,和常为5,那么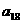 的值为________;若n为偶数,则这个数的前n项和Sn的计算公式为______________。
的值为________;若n为偶数,则这个数的前n项和Sn的计算公式为______________。
11.已知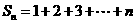 ,
,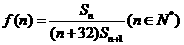 ,则
,则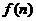 的最大值是________
的最大值是________
10.毛泽东在《送瘟神》中写到:“坐地日行八万里”,又知地球的体积大约是火星的8倍,则火星的大圆周长约为______________万里.
9.已知椭圆中心在原点,它在x轴上的一个焦点与短轴两端点的连线互相垂直,并且这个焦点到椭圆的最短距离为4(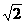 -1),则椭圆的方程为_________。
-1),则椭圆的方程为_________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com