
题目列表(包括答案和解析)
98.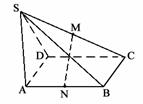 已知ABCD是矩形,SA⊥平面ABCD,M、N分别是SC、AB的中点.
已知ABCD是矩形,SA⊥平面ABCD,M、N分别是SC、AB的中点.
求证:MN⊥AB.
解析:连结MB、MA,证明MB=MA.
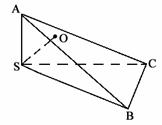
97. 已知:如图,AS⊥平面SBC,SO⊥平面ABC于O,
求证:AO⊥BC.
解析:连结AO,证明BC⊥平面ASO.
96. 已知PA,PB,PC与平面α所成的角分别为60°,45°,30°,PO⊥平面α,O为垂足,又斜足A,B,C三点在同一直线上,且AB=BC=10cm,求PO的长.
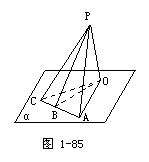
解析: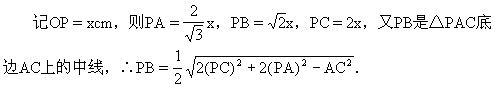
95. 已知:ABCD是矩形,SA⊥平面ABCD,E是SC上一点.
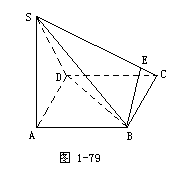
求证:BE不可能垂直于平面SCD.
解析:用到反证法,假设BE⊥平面SCD,
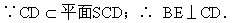
∵ AB∥CD;∴AB⊥BE.

∴ AB⊥SB,这与Rt△SAB中∠SBA为锐角矛盾.
∴ BE不可能垂直于平面SCD.
94. 已知E,F分别是正方形ABCD边AD,AB的中点,EF交AC于M,GC垂直于ABCD所在平面.
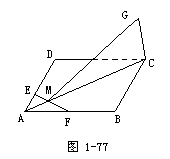
(1)求证:EF⊥平面GMC.
(2)若AB=4,GC=2,求点B到平面EFG的距离.
解析:第1小题,证明直线与平面垂直,常用的方法是判定定理;第2小题,如果用定义来求点到平面的距离,因为体现距离的垂线段无法直观地画出,因此,常常将这样的问题转化为直线到平面的距离问题.
解:
(1)连结BD交AC于O,
∵E,F是正方形ABCD边AD,AB的中点,AC⊥BD,
∴EF⊥AC.
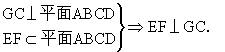
∵AC∩GC=C,
∴EF⊥平面GMC.
(2)可证BD∥平面EFG,由例题2,正方形中心O到平面EFG

93.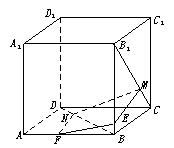 如图,在正方体ABCD-A1B1C1D1中,点N在BD上,点M在B1C上,并且CM=DN.
如图,在正方体ABCD-A1B1C1D1中,点N在BD上,点M在B1C上,并且CM=DN.
求证:MN∥平面AA1B1B.
解析:本题是把证“线面平行”转化为证“线线平行”,即在平面ABB1A1内找一条直线与MN平行,除上面的证法外,还可以连CN并延长交直线BA于点P,连B1P,就是所找直线,然后再设法证明MN∥B1P.
分析二:要证“线面平行”也可转化为证“面面平行”,因此,本题也可设法过MN作一个平面,使此平面与平面ABB1A1平行,从而证得MN∥平面ABB1A1.
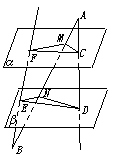
92. 已知:平面α∥平面β,线段AB分别交α、β于点M、N;线段AD分别交α、β于点C、D;线段BF分别交α、β于点F、E,且AM=m,BN=n,MN=p,△FMC面积=(m+p)(n+p),求:END的面积.
解析:如图,面AND分别交α、β于MC,ND,因为α∥β,
故MC∥ND,同理MF∥NE,得
∠FMC=∠END,
∴ND∶MC=(m+p):m和EN∶FM=n∶(n+p)
 S△END∶S△FMC=
S△END∶S△FMC=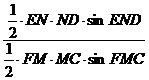
得S△END=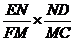 ×S△FMC
×S△FMC
=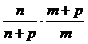 ·(m+p)(n+p)=
·(m+p)(n+p)=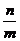 (m+p)2
(m+p)2
∴△END的面积为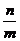 (m+p)2平方单位.
(m+p)2平方单位.
91. 如图,正方体ABCD-A1B1C1D1中,E在AB1上,F在BD上,且B1E=BF.
求证:EF∥平面BB1C1C.
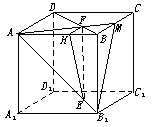 证法一:连AF延长交BC于M,连结B1M.
证法一:连AF延长交BC于M,连结B1M.
∵AD∥BC
∴△AFD∽△MFB
∴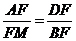
又∵BD=B1A,B1E=BF
∴DF=AE
∴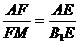
∴EF∥B1M,B1M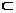 平面BB1C1C
平面BB1C1C
∴EF∥平面BB1C1C.
证法二:作FH∥AD交AB于H,连结HE
∵AD∥BC
∴FH∥BC,BC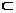 BB1C1C
BB1C1C
∴FH∥平面BB1C1C
由FH∥AD可得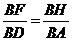
又BF=B1E,BD=AB1
∴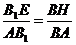
∴EH∥B1B,B1B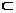 平面BB1C1C
平面BB1C1C
∴EH∥平面BB1C1C,
EH∩FH=H
∴平面FHE∥平面BB1C1C
EF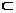 平面FHE
平面FHE
∴EF∥平面BB1C1C
说明:证法一用了证线面平行,先证线线平行.证法二则是证线面平行,先证面面平行,然后说明直线在其中一个平面内.
90. 三个平面两两相交得三条直线,求证:这三条直线相交于同一点或两两平行.
已知:平面α∩平面β=a,平面β∩平面γ=b,平面γ∩平面α=c.
求证:a、b、c相交于同一点,或a∥b∥c.
证明:∵α∩β=a,β∩γ=b
∴a、b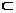 β
β
∴a、b相交或a∥b.
(1)a、b相交时,不妨设a∩b=P,即P∈a,P∈b
而a、b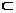 β,a
β,a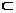 α
α
∴P∈β,P∈α,故P为α和β的公共点
又∵α∩γ=c
由公理2知P∈c
∴a、b、c都经过点P,即a、b、c三线共点.
(2)当a∥b时
∵α∩γ=c且a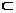 α,a
α,a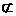 γ
γ
∴a∥c且a∥b
∴a∥b∥c
故a、b、c两两平行.
由此可知a、b、c相交于一点或两两平行.
说明:此结论常常作为定理使用,在判断问题中经常被使用.
89. 已知平面 、
、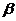 、
、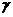 、
、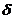 .其中
.其中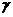 ∩
∩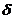 =l,
=l, ∩
∩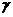 =a,
=a,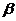 ∩
∩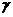 =
=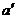 ,a∥
,a∥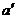 ,
, ∩
∩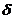 =b,
=b,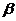 ∩
∩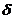 =
=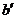 ,b∥
,b∥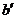
上述条件能否保证有 ∥
∥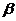 ?若能,给出证明,若不能给出一个反例,并添加适当的条件,保证有
?若能,给出证明,若不能给出一个反例,并添加适当的条件,保证有 ∥
∥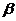 .
.
不足以保证 ∥
∥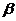 .
.
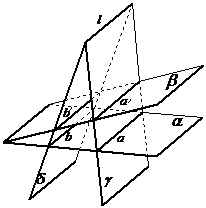 如右图.
如右图.
如果添加条件a与b是相交直线,那么 ∥
∥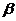 .
.
证明如下:
a∥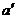
 a∥
a∥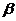
b∥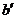
 b∥
b∥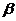
∵ a,b是 内两条相交直线,
内两条相交直线,
∴  ∥
∥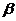 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com