
题目列表(包括答案和解析)
4、已知x、y的取值如下表:
|
x |
0 |
1 |
3 |
4 |
|
y |
2.2 |
4.3 |
4.8 |
6.7 |
从散点图分析,y与x线性相关,且回归方程为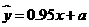 ,则
,则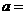
3、设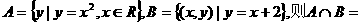
2、命题“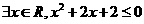 ”的否定是
”的否定是
1、复数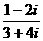 在复平面上对应的点位于第__ 象限.
在复平面上对应的点位于第__ 象限.
(15) 半径为5的圆过点A(-2,
6),且以M(5, 4)为中点的弦长为2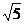 ,求此圆的方程。
,求此圆的方程。
(16) 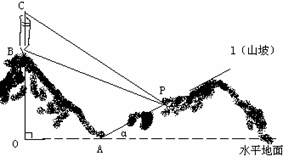 某人在一山坡P处观看对面山项上的一座铁塔,如图所示,塔高BC=80(米),塔所在的山高OB=220(米),OA=200(米),图中所示的山坡可视为直线l且点P在直线l上,
某人在一山坡P处观看对面山项上的一座铁塔,如图所示,塔高BC=80(米),塔所在的山高OB=220(米),OA=200(米),图中所示的山坡可视为直线l且点P在直线l上, 与水平地面的夹角为
与水平地面的夹角为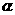 ,
, 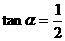 试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)
试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)
(17) 已知定点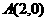 ,
,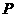 点在圆
点在圆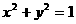 上运动,
上运动, 的平分线交
的平分线交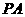 于
于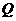 点,其中
点,其中 为坐标原点,求
为坐标原点,求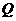 点的轨迹方程.
点的轨迹方程.
(18) 已知圆C: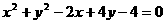 ,是否存在斜率为1的直线l,使l被圆C截得的弦AB为直径的圆过原点,若存在求出直线l的方程,若不存在说明理由。
,是否存在斜率为1的直线l,使l被圆C截得的弦AB为直径的圆过原点,若存在求出直线l的方程,若不存在说明理由。
(11) 已知圆 交于A、B两点,则AB所在的直线方程是__________。
交于A、B两点,则AB所在的直线方程是__________。
(12)直线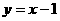 上的点到圆
上的点到圆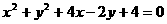 的最近距离是
。
的最近距离是
。
(13)已知圆的方程是x2+y2=1,则在y轴上截距为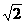 的切线方程为
。
的切线方程为
。
(14)过P(-2,4)及Q(3,-1)两点,且在X轴上截得的弦长为6的圆方程是______
(1) 平行四边形ABCD的一条对角线固定在A(3,-1),C(2,-3)两点,D点在直线3x-y+1=0上移动,则B点轨迹所在的方程为 ( )
A 3x-y-20=0 B 3x-y-10=0 C 3x-y-9=0 D 3x-y-12=0
(2)若方程x+y-6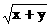 +3k=0仅表示一条射线,则实数k的取值范围是
(
)
+3k=0仅表示一条射线,则实数k的取值范围是
(
)
A (-∞,3)
B (-∞,0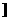 或k=3 C
k=3
D (- ∞,0)或k=3
或k=3 C
k=3
D (- ∞,0)或k=3
(3)入射光线沿直线x-2y+3=0射向直线l: y=x被直线反射后的光线所在的方程是 ( )
A x+2y-3=0 B x+2y+3=0
C 2x-y-3=0 D 2x-y+3=0
(4) “a=b”是“直线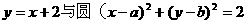 相切”的
(
)
相切”的
(
)
A 充分不必要条件 B 必要不充分条件
C 充分必要条件 D 既不充分又不必要条件
(5) 设集合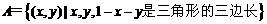 ,则A所表示的平面区域(不含边界的阴影部分)是 ( )
,则A所表示的平面区域(不含边界的阴影部分)是 ( )
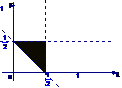
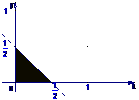
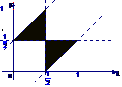
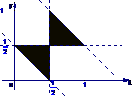
A B C D
(6)由动点P向圆x2 + y2=1引两条切线PA、PB,切点分别为A、B,∠APB=60°,则动点P的轨迹方程为 ( )
A x2+y2=4 B x2+y2=3 C x2+y2=2 D x2+y2=1
(7) 从原点向圆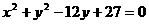 作两条切线,则这两条切线的夹角的大小为 ( )
作两条切线,则这两条切线的夹角的大小为 ( )
A 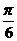 B
B
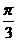 C
C
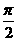 D
D
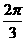
(8)已知圆x2+y2+2x-6y+F=0与x+2y-5=0交于A, B两点, O为坐标原点, 若OA⊥OB, 则F
的值为 ( )
A 0 B 1 C -1 D 2
(9) 若圆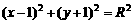 上有且仅有两个点到直线4x+3y=11的距离等于1,则半径R的取值范围是
( )
上有且仅有两个点到直线4x+3y=11的距离等于1,则半径R的取值范围是
( )
A R>1 B R<3 C 1<R<3 D R≠2
(10) 已知直线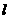 过点
过点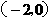 ,当直线
,当直线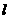 与圆
与圆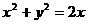 有两个交点时,其斜率k的取值范围是
( )
有两个交点时,其斜率k的取值范围是
( )
A 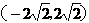 B
B 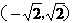 C
C 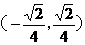 D
D 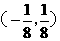
(15)点A、B分别是椭圆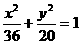 长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于
长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于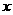 轴上方,
轴上方,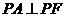 .求点P的坐标;
.求点P的坐标;
.
(16) 已知抛物线C: y=-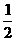 x2+6, 点P(2, 4)、A、B在抛物线上, 且直线PA、PB的倾斜角互补.
x2+6, 点P(2, 4)、A、B在抛物线上, 且直线PA、PB的倾斜角互补.
(Ⅰ)证明:直线AB的斜率为定值;
(Ⅱ)当直线AB在y轴上的截距为正数时, 求△PAB面积的最大值及此时直线AB的方程.
(17) 双曲线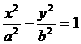 (a>1,b>0)的焦距为2c,直线l过点(a,0)和(0,b),且点(1,0)到直线l的距离与点(-1,0)到直线l的距离之和s≥
(a>1,b>0)的焦距为2c,直线l过点(a,0)和(0,b),且点(1,0)到直线l的距离与点(-1,0)到直线l的距离之和s≥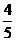 c.求双曲线的离心率e的取值范围
c.求双曲线的离心率e的取值范围
(18) 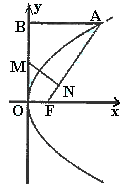 已知抛物线
已知抛物线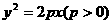 的焦点为F,A是抛物线上横坐标为4、且位于
的焦点为F,A是抛物线上横坐标为4、且位于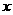 轴上方的点,A到抛物线准线的距离等于5.过A作AB垂直于
轴上方的点,A到抛物线准线的距离等于5.过A作AB垂直于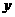 轴,垂足为B,OB的中点为M.
轴,垂足为B,OB的中点为M.
(1)求抛物线方程;
(2)过M作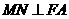 ,垂足为N,求点N的坐标;
,垂足为N,求点N的坐标;
(3)以M为圆心,MB为半径作圆M,当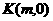 是
是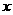 轴上一动点时,讨论直线AK与圆M的位置关系.
轴上一动点时,讨论直线AK与圆M的位置关系.
(11) 若双曲线的渐近线方程为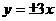 ,它的一个焦点是
,它的一个焦点是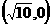 ,则双曲线的方程是__________.
,则双曲线的方程是__________.
(12)设中心在原点的椭圆与双曲线2 x2-2y2=1有公共的焦点,且它们的离心率互为倒数,则该椭圆的方程是 .
(13) 过双曲线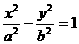 (a>0,b>0)的左焦点且垂直于x轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于_________.
(a>0,b>0)的左焦点且垂直于x轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于_________.
(14) 以下同个关于圆锥曲线的命题中
①设A、B为两个定点,k为非零常数,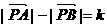 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②过定圆C上一定点A作圆的动弦AB,O为坐标原点,若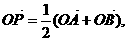 则动点P的轨迹为椭圆;
则动点P的轨迹为椭圆;
③方程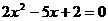 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④双曲线 有相同的焦点.
有相同的焦点.
其中真命题的序号为 (写出所有真命题的序号)
(1) 抛物线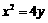 上一点
上一点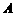 的纵坐标为4,则点
的纵坐标为4,则点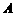 与抛物线焦点的距离为
(
)
与抛物线焦点的距离为
(
)
A 2 B 3 C 4 D 5
(2) 若焦点在x轴上的椭圆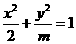 的离心率为
的离心率为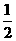 ,则m=
(
)
,则m=
(
)
A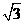 B
B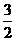 C
C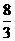 D
D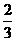
(3) 若方程x2+ky2=2表示焦点在y轴上的椭圆, 那么实数k的取值范围是 ( )
A (0, +∞) B (0, 2) C (1, +∞) D (0, 1)
(4) 设P是双曲线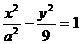 上一点,双曲线的一条渐近线方程为
上一点,双曲线的一条渐近线方程为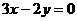 ,F1、F2分别是双曲线的左、右焦点,若
,F1、F2分别是双曲线的左、右焦点,若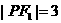 ,则
,则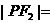 (
)
(
)
A 1或5 B 6 C 7 D 9
(5) 对于抛物线y2=2x上任意一点Q, 点P(a, 0)都满足|PQ|≥|a|, 则a的取值范围是 ( )
A [0, 1]
B (0, 1)
C 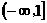 D
(-∞, 0)
D
(-∞, 0)
(6) 若椭圆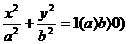 的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx的焦点分成5:3两段,则此椭圆的离心率为 ( )
的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx的焦点分成5:3两段,则此椭圆的离心率为 ( )
A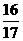 B
B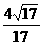 C
C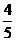 D
D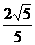
(7) 已知双曲线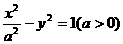 的一条准线与抛物线
的一条准线与抛物线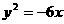 的准线重合,则该双曲线的离心率为 ( )
的准线重合,则该双曲线的离心率为 ( )
A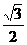 B
B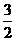 C
C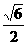 D
D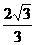
(8) 设A(x1,y1),B(x2,y2)是抛物线y2=2px(p>0)上的两点,并且满足OA⊥OB. 则y1y2等于( )
A – 4p2 B 4p2 C – 2p2 D 2p2
(9) 已知双曲线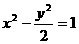 的焦点为F1、F2,点M在双曲线上且
的焦点为F1、F2,点M在双曲线上且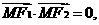 则点M到x轴的距离为
( )
则点M到x轴的距离为
( )
A
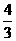 B
B
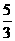 C
C
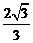 D
D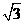
(10) 设椭圆的两个焦点分别为F1、、F2,过F2作椭圆长轴的垂线交椭圆于点P,
若△F1PF2为等腰直角三角形,则椭圆的离心率是 ( )
A
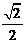 B
B
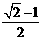 C
C
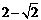 D
D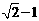
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com