
题目列表(包括答案和解析)
1对称问题分类:
|
对称问题分类 |
解法 |
|
(1).点关于点对称 |
中点坐标公式 |
|
(2).直线关于点对称 |
转化为(1)解决或代入法 |
|
(3).点关于直线对称 |
中点在对称直线上,连线和对称直线垂直, 简记为“垂直平分 |
|
(4)直线关于直线对称 |
转化为(3)解决或代入法 |
说明:(1).光线反射问题即是对称问题。
(2) 需要记住的特殊情况:与Ax+By+C=0关于x轴对称 Ax-By+C=0,
关于y轴对称-Ax+By+C=0,关于原点对称-Ax-By+C=0,关于y=x对称
Bx+Ay+C=0,关于y=-x对称 -Bx-Ay+C=0。
2.典型练习:
已知点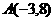 、
、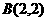 ,点
,点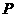 是
是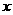 轴上的点,求当
轴上的点,求当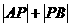 最小时的点
最小时的点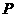
的坐标.
略解:点A关于x轴的对称点为A′(-3,-8),
A′B:2x-y-2=0,A′B与x轴交点为 P(1,0)即为所求.
2.典型练习:
(1).正方形中心在C(-1,0),一条边方程为: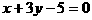 ,求其余三边直线方程.
,求其余三边直线方程.
(2).直线kx-y+1=3k,当k变动时,所有直线都通过定点( )
A.(0,0) B.(0,1) C.(3,1) D.(2,1)
答案:(1).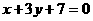 ,
,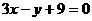 ,
,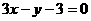
(2). C
1.直线系分类:
(1).平行直线系:与Ax+By+C=0的直线可设为平行Ax+By+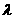 =0(
=0(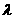 ≠C)
≠C)
(2).垂直直线系:与Ax+By+C=0的垂直直线可设为Bx-Ay+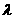 =0
=0
(3).过定点的直线系:过定点P(x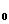 ,
y
,
y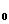 )的直线可设为x= x
)的直线可设为x= x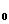 或y- y
或y- y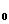 =k(x- x
=k(x- x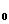 )
)
(4)过两条直线交点的直线系:经过L :A
:A x+B
x+B y+C
y+C =0和L
=0和L :A
:A x+B
x+B y+C
y+C =0交点的直线可设为A
=0交点的直线可设为A x+B
x+B y+C
y+C +
+ 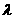 (A
(A x+B
x+B y+C
y+C )=0
)=0
4.典型练习:
(1)..过点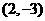 ,且与
,且与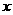 轴,
轴,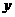 轴的截距相等的直线方程是
_____________________ .
轴的截距相等的直线方程是
_____________________ .
(2)..经过点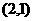 的直线
的直线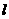 到A
到A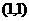 、B
、B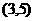 两点的距离相等,则直线
两点的距离相等,则直线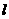 的方程为 ( )
的方程为 ( )
A.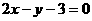 B.
B.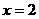
C.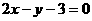 或
或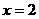 D.都不对
D.都不对
答案(1)..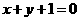 或
或 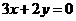
(2).C(数形结合法或待定系数法)
3.易错点:
(1).点斜式易忽略无截距,造成丢解
(2).截距式易忽略无斜率不存在,造成丢解
2.求直线方程的方法:
(1).设点、求点利用两点式
(2).设直线方程,利用待定系数法。
(3).数形结合法,画出符合条件的直线,根据其特点直接写方程。
注意:求出直线方程后一般要化为一般式或点斜式,这是约定俗成的。
1.五种形式:
(1)点斜式: y- y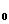 =k(x- x
=k(x- x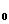 )
)
(2)斜截式: y=kx+b
(3)两点式: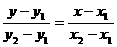 ( x
( x ≠x
≠x ,y
,y ≠y
≠y )
)
(4)截距式: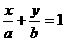
(5)一般式: Ax+By+C=0(A、B不能同时为0)
五种形式各有优点和局限性,要根据实际情况灵活选择,一般常用的是点斜式和斜截式。
2.(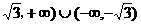
2.已知直倾斜角的范围是(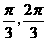 ),则斜率的取值范围是
),则斜率的取值范围是
答案:1. [0°,30°]∪[150°,180°).
5.典型练习:1.设θ∈R,则直线xsinθ-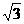 y+1=0的倾斜角的取值范围为____________________________________
y+1=0的倾斜角的取值范围为____________________________________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com