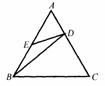
9．如图9，在正三角形ABC中，D、E分别在AC、AB上，且AD：AC=1：3，AE=BE，则有(　 )

△AED∽△BED (B)△AED∽△CBD

(C)△AED∽△ABD (D)△BAD∽△BCD

(第5题)　　　 (第6题)　　　　 (第7题)　　　　 (第8题)　　　 (第9题)

8．如图8，已知△ADE∽△ABC，相似比为2：3，则=(　 )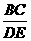

(A)3：2　　 (B)2：3 　(C) 2：1 　　(D)不能确定

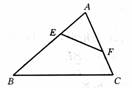
7．如图7，平行四边形ABCD中，G是BC延长线上一点，AG与BD交于点E，与DC交于点F，

则图中相似三角形有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

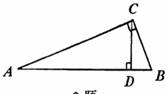
6．如图6，在△ABC中，点D在线段BC上，∠BAC=∠ADC，AC=8，BC=16，那么CD=__________。

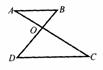
4．如图，线段AC、BD相交于点O，要使△AOB∽△DOC，已具备条件　　　　　 　还需补充的条件是　 　　　　　　　或　　　　　　　 　或　　　　　　　　 　

　　 (第1题)　　　　 (第2题)　　　　 (第3题)　　　　 (第4题)　　　　

5．如图5，AB∥DC，AC交BD于点O．已知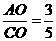，BO＝6，则DO=_________。

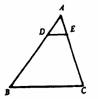
3．如图3，要使△AEF∽△ACB，已具备条件　　　　　 　还需补充的条件是　　　　　　 　，或　　　　　　　 　，或　 　　　　　　　

2．如图2，在ΔABC中，∠ACB=90°，CD⊥AB，垂足为D，AC=12，BC=5，则CD的长是　　　　　

1．如图1，D,E分别是△ABC的边AC,AB上的点，当△AED和△ACB满足条件　　　　 时，使得△AED-△ACB.(填上你认为正确的一种条件即可，不必考虑所有可能的情形)

18、如图，矩形ABCD中，E为BC上一点，DF⊥AE于F.

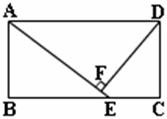(1)ΔABE与ΔADF相似吗？请说明理由.

(2)若AB=6，AD=12，BE=8，求DF的长. (11分)

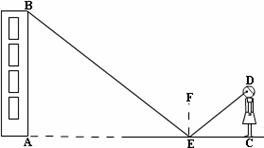
17、小玲用下面的方法来测量学校教学大楼AB的高度：

如图，在水平地面上放一面平面镜，镜子与教学大楼的距离EA=21米.当她与镜子的距离CE=2.5米时，她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.6米.请你帮助小玲计算出教学大楼的高度AB是多少米(注意：根据光的反射定律：反射角等于入射角).10分