
题目列表(包括答案和解析)
4. (x2-px+3)(x-q)的乘积中不含x2项,则( ) A.p=q B.p=±q C.p=-q D.无法确定
3. 计算(2x-3y)(4x2+6xy+9y2)的正确结果是( ) A.(2x-3y)2 B.(2x+3y)2 C.8x3-27y3 D.8x3+27y3
2. 若(x+a)(x+b)=x2-kx+ab,则k的值为( ) A.a+b B.-a-b C.a-b D.b-a
1. 计算(2a-3b)(2a+3b)的正确结果是( )
A.4a2+9b2 B.4a2-9b2 C.4a2+12ab+9b2 D.4a2-12ab+9b2
9.巧拆项
例10 解不等式
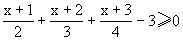
分析 将-3拆为三个负1,再分别与另三项结合可巧解本题.
解 原不等式变形为
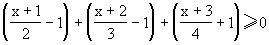
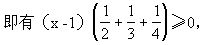
得x-1≥0,故x≥1.
练习题
解下列一元一次不等式
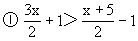
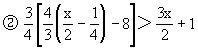
③3{3x+2-[2(3x+2)-1]}≥3x+1.
8.巧用整体合并
例9 解不等式
3{2x-1-[3(2x-1)+3]}>5.
解 视2x-1为一整体,去大、中括号,得3(2x-1)-9(2x-1)-9>5,整体合并,得-6(2x-1)>14,
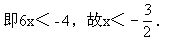
7.逆用乘法分配律
例8 解不等式
278(x-3)+351(6-2x)-463(3-x)>0.
分析 直接去括号较繁,注意到左边各项均含有因式x-3而逆用分配律可速解此题.
解 原不等式化为
(x-3)(278-351×2+463)>0,
即 39(x-3)>0,故x>3.
6.巧去括号
去括号一般是内到外,即按小、中、大括号的顺序进行,但有时反其道而行之即由外到内去括号往往能另辟捷径.
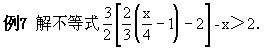

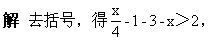
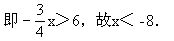
5.巧用分数基本性质
例5 解不等式
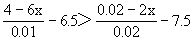

约去公因数2后,两边的分母相同;②两个常数项移项合并得整数.
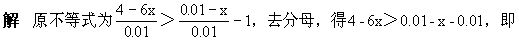
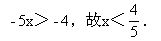
例6 解不等式
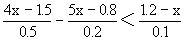
分析 由分数基本性质,将分母化为整数和去分母一次到位可避免繁琐的运算.
解 原不等式为
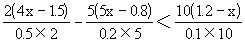
整理,得8x-3-25x+4<12-10x,
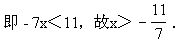
思考:例5可这样解吗?请不妨试一试.
4.逆用分数加减法法则
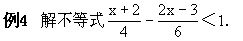
解 原不等式化为
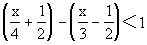 ,
,
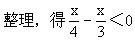
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com