
题目列表(包括答案和解析)
2、当x __________时分式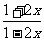 有意义。
有意义。
1、分式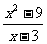 当x __________时分式的值为零。
当x __________时分式的值为零。
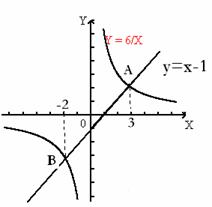
25、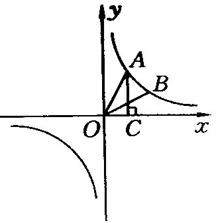 解:(1)∵A点在反比例函数
解:(1)∵A点在反比例函数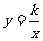 的图象上,∴设点A的坐标为A(
的图象上,∴设点A的坐标为A(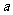 ,
,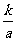 ),由
),由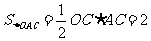 ,得
,得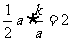 ,即
,即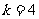 。
。
∴所求反比例函数的解析式为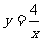 。
。
(2)∵ ,∴
,∴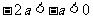 。∵点(-a,y1)、(-2a,y2)在反比例函数
。∵点(-a,y1)、(-2a,y2)在反比例函数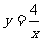 的图象上,且都在第三象限的分支上,而该函数图象在第三象限
的图象上,且都在第三象限的分支上,而该函数图象在第三象限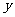 随
随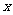 的增大而减小,
的增大而减小,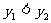 。
。
(3)作BD⊥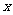 轴,垂足为点D,
轴,垂足为点D,
∵B点在反比例函数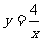 的图象上,∴B点的坐标为(
的图象上,∴B点的坐标为(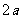 ,
,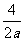 ),
),
∴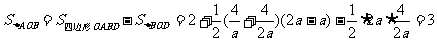
24、解:(1)根据题意,AB=x,AB·BC=60,所以BC=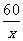 。
。
y=20×3(x+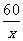 )+80×3(x+
)+80×3(x+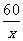 )
)
即y=300(x+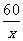 ).
).
(2)把y=4 800代入y=300(x+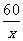 )可得:4 800=300(x+
)可得:4 800=300(x+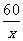 ).
).
整理得x2-16x+60=0.
解得x1=6,x2=10.
经检验,x1=6,x2=10都是原方程的根.
由8≤x≤12,只取x=10.
所以利用旧墙壁的总长度10+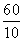 =16m.
=16m.
23、解:(1)设A点坐标为(x,y),且x<0,y>0则
S△ABO=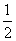 ·│BO│·│BA│=
·│BO│·│BA│=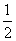 ·(-x)·y=
·(-x)·y=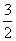 。
。
∴xy=-3.
又∵y=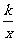 ,即xy=k,∴k=-3.
,即xy=k,∴k=-3.
∴所求的两个函数的解析式分别为y=-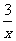 ,y=-x+2.
,y=-x+2.
(2)由y=-x+2,令y=0,得x=2.
∴直线y=-x+2与x轴的交点D的坐标为(2,0).
再由
∴交点A为(-1,3),C为(3,-1).
∴S△AOC=S△ODA+S△ODC=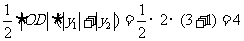 。
。
22、解:(1)设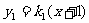 ,
,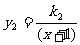 ;则有:
;则有: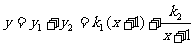
∵当x=0时,y=-5;当x=2时,y=-7;
∴有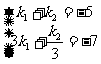 解得:
解得: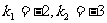 ;
;
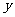 与
与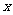 的函数关系式为:
的函数关系式为: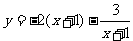 ;
;
(2)把y=5代入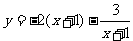 可得:
可得: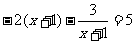
解得: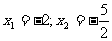 。(检验:略)
。(检验:略)
21、解:(1)联立解析式: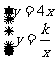 ,可得:
,可得: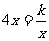 ,∵
,∵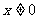 ∴
∴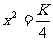 ;
;
若两个函数的图象有两个交点,则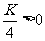 ,解得:
,解得: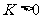 ;
;
若两个函数的图象没有交点,则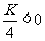 ,解得:
,解得: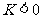
(2)∵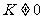 ∴两个函数的图象不可能只有一个交点。
∴两个函数的图象不可能只有一个交点。
20、解:(1)函数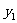 的自变量取值范围是:全体实数,函数
的自变量取值范围是:全体实数,函数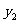 的自变量取值范围是:
的自变量取值范围是: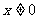 ,列表可得:
,列表可得:
|
x |
… |
-5 |
-4 |
-3 |
-2 |
-1 |
1 |
2 |
3 |
4 |
5 |
… |
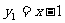 |
… |
-6 |
-5 |
-4 |
-3 |
-2 |
0 |
1 |
2 |
3 |
4 |
… |
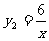 |
… |
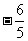 |
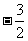 |
-2 |
-3 |
-6 |
6 |
3 |
2 |
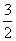 |
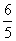 |
… |
(2)联立解析式: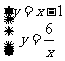 解得:
解得: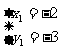 ,
,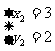
∴两函数的交点坐标分别为A(-2,-3);B(3,2);
(3)由图象观察可得:当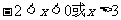 时,
时,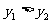 。
。
19、解:(1)∵点P(x0,3)在一次函数y=x+m的图象上.
∴3=x0+m,即m=3-x0.
又点P(x0,3)在反比例函数y=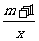 的图象上.
的图象上.
∴3=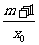 ,即m=3x0-1. ∴3-x0=3x0-1,解得x0=1.
,即m=3x0-1. ∴3-x0=3x0-1,解得x0=1.
(2)由(1),得m=3-x0=3-1=2, ∴一次函数的解析式为y=x+2,
反比例函数的解析式为y=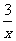
18、解:(1)依题意可得: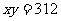 ;∴
;∴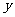 关于
关于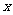 的函数关系式是
的函数关系式是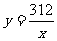 ;
;
(2)把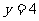 代入
代入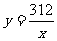 可得:
可得: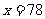 ;
;
∴提速后列车的速度为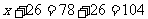 ;
;
当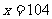 时,
时,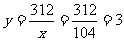 ;
;
答:提速后从甲站到乙站需要3个小时。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com