(五)小结：

(四)例题分析

例1求证:全等三角形对应角的平分线相等.

证明命题的一般步骤:

(1)根据题意,画出图形;

(2)用符号语言写出“已知”和“求证”;

(3)分析证明思路;

(4) 写出证明过程;

例2已知：如图，△ABC中,∠C=2∠B，∠BAD=∠DAC.

　 求证：AB=AC+CD

还有其他方法吗？

A　　　　　　　　　　　　　　　　　　　　　　　　 A

E

B　　 　　　D　　　 　　C　　　 　　　　B　　　　　　 D　　　　　　　　 C

　(第三题)　 　　　　　　　　　　　　　　　　(第二题)

例3已知 ：如图D,E分别是BC,AB上的一点,BC、BD的长度之比为3:1, △ECD的面积是△ABC的面积的一半.

求证： BE=3AE

例4、已知：如图，直线AB，CD，EF在同一平面内，且AB ∥ EF，CD ∥ EF，

求证：AB ∥ CD。

证明：假设AB∥CD,那么AB与CD一定相交于一点P

∵AB ∥ EF，CD ∥ EF(已知)

∴过点P有两条直线AB， CD都与直线EF平行。

这与“经过直线外一点，有一条而且只有一条直线和这条直线平行”矛盾。

∴AB ∥ CD不能成立。

∴AB ∥ CD

反证法的一般步骤：

1.反设(否定结论)；

2.归谬(利用已知条件和反设，进行推理，得出与已学过的公理、定理、定义或与已知条件矛盾)；

3.写出结论(肯定原命题成立)。

练习：

如图,已知:AB=AE，BC=DE， ∠B= ∠E,

　　　　　　　　 AF⊥CD于F.

　　 求证:CF=DF.

(三)练一练

1. 用反例证明下列命题是假命题：

(1) 若x(5-x)=0，则x=0；

(2) 等腰三角形一边上的中线就是这条边上的高；

(3) 相等的角是内错角；

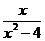
(4)若x≠2,则分式　　　 有意义.

(二)说一说

1.指出下列句子，哪些是命题，哪些不是命题？

(1)有两个角和夹边对应相等的三角形是全等的三角形；

(2)有两条边对应相等的两个三角形全等；

(3)作∠A的平分线；

(4)若a＝b　则　 a²= b²

(5) 同位角相等吗?

　2.说出一个已学过定理:

说出一个已学过公理:

3、下列把命题改写成“如果……，那么……”的形式。并判断下列命题的真假.

(1)不相等的角不可能是对顶角.

(2)垂直于同一条直线的两直线平行；

(3)两个无理数的乘积一定是无理数.

(一)知识回顾

1、一般地，对某一件事情作出正确或不正确的判断的句子叫做命题。

命题分为真命题与假命题。

2、说明一个命题是假命题,通常只用找出一个反例,但要说明一个命题是真命题,就必须用推理的方法,而不能光凭一个例子。

6、初步会综合运用命题、证明以及相关知识解决简单的实际问题。

5、通过实例，体会反证法的含义。了解反证法的基本步骤。

4、会根据一些基本事实证明简单命题。

2、会在简单情况下判断一个命题的真假。理解反例的作用，知道利用反例可证明一个命题是错误的。

3、了解证明的含义，理解证明的必要性，体会证明的过程要步步有据。

1、了解定义、命题、定理的含义，会区分命题的条件(题设)和结论。