前面我们已经学习了一次函数，那么什么是一次函数，一次函数的图像是什么，一次函数又有什么性质呢？

　　 表达式形如 y=kx+b(k=0)的函数称为一次函数；

　　 一次函数 y=kx+b的图像是一条直线；

　　 一次函数y=kx+b，当k＞0时y随x的增大而增大，图像经过一、三象限；

　　 当k＜0时y随x的增大而减小，图像经过二、四象限。

　　 确定一次函数的表达式是本章教材的一个重、难点，学生往往会按老师讲述的方法，单纯地进行模仿，求出表达式，但却对为什么要这样做缺乏思考，结果是条件一变，就无法动手。因此在教学中应注重对解题思路的分析，注意控制难度。

　　 教材前几节内容已对一次函数的表达式、函数图像及性质作了一定研究，给定一个一次函数的表达式可以得到对应的函数图像及性质，而本节则从相反角度来研究一次函数：即根据图像、表格等信息，确定一次函数的表达式。教材首先安排了想一想，让学生思考确定一次函数需要几个条件，教师可组织学生讨论陈述理由，从函数表达式及图像等方面让学生深刻理解两个条件确定一个一次函数。教学中应尽可能多的选择各种类型的信息帮助学生探索确定一次函数表达式的具体方法。

　　 教学重点：　　 能根据两个条件确定一个一次函数。

　　 教学难点：　　 从各种问题情境中寻找条件，确定一次函数的表达式。

2．经历对实际问题的解决过程，培养学生学数学，用数学的意识。

1．经历从不同信息中获取-次函数表达式的过程，体会到解决问题的多样性，培养学生思维的全面性。

3．能利用所学知识解决实际问题。

　　 过程与方法目标

　　 经历对正比例函数及一次函数表达式的探求过程，培养学生对数学对象进行思考的习惯，逐步培养学生的探索能力。

　　 情感与态度目标

2．能根据所给信息(图像、表格、实际问题等)确定一次函数的表达式。

　　 知识与技能目标

1．了解两个条件确定一次函数。

24.7 线段垂直平分线的性质定理及其逆定理

第1题. 如图，△ABC中，∠CAB=120º，AB，AC的垂直平分线分别交BC于点E、F，则∠EAF等于(　)

A．40º　 B．50º　 C．60º　 D．80º

答案：C．

第2题. 已知线段AB和它外一点P，若PA=PB，则点P在AB的____________________；若点P在AB的____________________，则PA=PB．

答案：垂直平分线上；垂直平分线上．

第3题. 已知：△ABC中，边AB，AC的垂直平分线相交于点P．

求证：点P在BC的垂直平分线上．

答案：连结PA，PB，PC，PB=PA=PC，所以，点P在BC的垂直平分线上．

第4题. ⑴作一个钝角三角形，利用尺规作这个三角形三条边的垂直平分线；

⑵作直角三角形和锐角三角形，利用尺规作三角形三条边的垂直平分线；

⑶你发现三角形三条边的垂直平分线与三角形的形状有怎样的位置关系？

答案：⑴、⑵略；⑶锐角三角形三边的垂直平分线的交点在三角形内部；直角三角形三边的垂直平分线的交点在斜边上，即斜边的中点；钝角三角形三边的垂直平分线的交点在三角形外部．

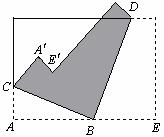
第5题. 将一张长方形纸片按如图所示的方式折叠，BC，BD为折痕，则∠CBD的度数为(　)

A．60° B．75°

C．90° D．95°

答案：C．

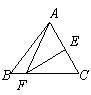第6题. 如图，在△ABC中，EF是AC的垂直平分线，AF=12，BF=3，则BC=__________．

答案：15．

第7题. 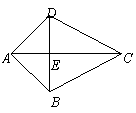如图，四边形ABCD中，AB=AD，BC=CD，AC，BD相交于E，由这些条件你能推出哪些结论(不再添加辅助线，不再标注字母，不写推理过程，只要求写出四个你认为正确的结论)？

答案：AC平分对角；AC⊥BD；AC平分BD；△ABC≌△ACD等．

第8题. 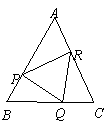如图，△ABC中，AB=AC，点P、Q、R分别在AB，BC，AC上，且PB=QC，QB=RC．

求证：点Q在PR的垂直平分线上．

答案：提示：AB=AC，∴∠B=∠C，又PB=QC，QB=RC，∴△BPQ≌△CQR，∴QP=QR，∴点Q在PR的垂直平分线上．

第9题. 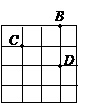把16个边长为a的正方形拼在一起，如图，连接BC，CD，则△BCD是(　)

A．直角三角形　 B．等腰三角形

C．等边三角形　 D．任意三角形

答案：B．

第10题. 若一个三角形两边的垂直平分线的交点在第三边上，则这个三角形是(　)

A．锐角三角形　 B．钝角三角形　 C．直角三角形　 D．不能确定

答案：C．