
题目列表(包括答案和解析)
9. 若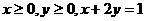 ,那么
,那么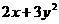 的最小值为__________________
的最小值为__________________
8.若函数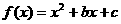 对任意实数都有
对任意实数都有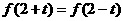 那么 ( )
那么 ( )
(A)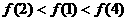 (B)
(B)
(C)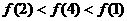 (D)
(D)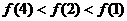
7.已知函数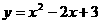 在必区间
在必区间 上有最大值3,最小值2,则
上有最大值3,最小值2,则 的取值范围是
( )
的取值范围是
( )
(A) 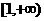 (B)
(B)
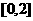 (C)
(C)
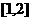 (D)
(D)
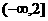
6.如果实数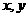 满足
满足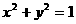 ,那么
,那么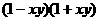 有 ( )
有 ( )
(A)最大值为
1 , 最小值为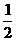 (B)无最大值,最小值为
(B)无最大值,最小值为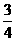
(C))最大值为
1, 无最小值 (D)最大值为1,最小值为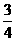
5. 函数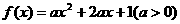 在区间
在区间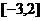 上有最大值4,则
上有最大值4,则 ____________
____________
4. 若函数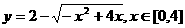 的值域是______________________
的值域是______________________
3.函数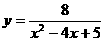 的最值为
( )
的最值为
( )
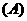 最大值为8,最小值为0
最大值为8,最小值为0 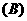 不存在最小值,最大值为8
不存在最小值,最大值为8
(C)最小值为0, 不存在最大值 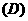 不存在最小值,也不存在最大值
不存在最小值,也不存在最大值
1函数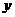
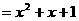 在
在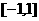 上的最小值和最大值分别是
( )
上的最小值和最大值分别是
( ) 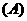 1 ,3
1 ,3 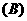
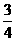 ,3 (C)
,3 (C)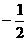 ,3 (D)
,3 (D)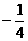 , 3
, 3
2.函数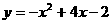 在区间
在区间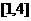 上的最小值是
( )
上的最小值是
( )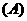
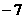
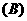


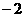
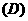 2
2
闭区间上二次函数的最值问题可分以下几种类型:
(1) 定区间、定对称轴;--配方、判定对称轴与区间的位置关系、确定最值。
(2) 定区间、动对称轴;--分对称轴在区间左、区间中、区间右(或区间中点左、区间中 点右)讨论。
(3) 动区间、定对称轴;--分对称轴在区间左、区间中、区间右(或区间中点左、区间中 点右)讨论。
注意:
(1) 分类讨论的划分标准;
(2) 数形结合的助于讨论;
(3) 倒过来思考有时更有助于问题的解决。
例1:求函数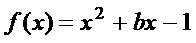 ,
,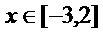 的最大值与最小值。
的最大值与最小值。
例2:设函数 在区间
在区间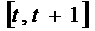 上的最小值是
上的最小值是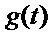 ,最大值是
,最大值是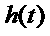 ,分别求
,分别求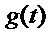 和
和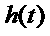 的解析式。
的解析式。
例3:根椐下列条件求实数a的值:
(1)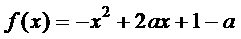 在[0,1]上有最大值2;
在[0,1]上有最大值2;
(2)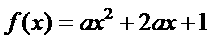 在[-3,2]上有最大值4。
在[-3,2]上有最大值4。
思考:
已知函数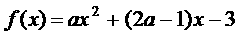 在
在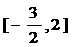 有最大值1,求实数a的值。
有最大值1,求实数a的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com