
题目列表(包括答案和解析)
1、下列函数有2个零点的是( )
A、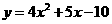 B、
B、
C、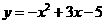 D、
D、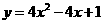
2,方程x-1=lgx必有一个根的区间是( )
A, (0.1 ,0.2) B,(0.2,0.3) C,(0.3,0.4) D,(0.4,0.5)
3,函数y=(0.5)x与函数y=lgx的图象的交点的横坐标(精确到0.1)约是( )
A,1.3 B,1.4 C,1.5 D,1.6
4,某工厂10年来某种产品总产量C与时间t(年)的函数关系如下图所示,下列四种说法,其中说法正确的是( )
①前五年中产量增长的速度越来越快 ②前五年中产量增长的速度越来越慢 ③第五年后,这种产品停止生产 ④第五年后,这种产品的产量保持不变
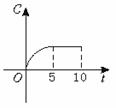 A.②③ B.②④
C.①③ D.①④
A.②③ B.②④
C.①③ D.①④
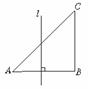
5下图△ABC为等腰直角三角形,直线l与AB相交且l⊥AB,直线l截这个三角形所得的位于直线右方的图形面积为y,点A到直线l的距离为x,则y=f(x)的图象大致为( )

6,已知实数a、b、c是图象连续不断的函数y=f(x)定义域中的三个数,且满足a<b<c
,f(a).f(b)<0, f(b).f(c)<0,则函数y=f(x)在区间(a,c)上的零点个数为( )
A, 2 B,奇数 C,偶数 D,至少是2
1 已知
已知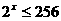 且
且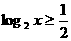 ,求函数
,求函数 的最大值和最小值
的最大值和最小值
2 建造一个容积为
建造一个容积为 立方米,深为
立方米,深为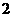 米的无盖长方体蓄水池,池壁的造价为每平方米
米的无盖长方体蓄水池,池壁的造价为每平方米 元,池底的造价为每平方米
元,池底的造价为每平方米 元,把总造价
元,把总造价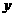 (元)表示为底面一边长
(元)表示为底面一边长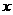 (米)的函数
(米)的函数
3 已知
已知 且
且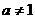 ,求使方程
,求使方程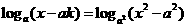 有解时的
有解时的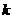 的取值范围
的取值范围
(数学1必修)第三章 函数的应用 [提高训练C组]
1 函数
函数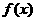 对一切实数
对一切实数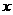 都满足
都满足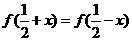 ,并且方程
,并且方程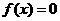 有三个实根,则这三个实根的和为
有三个实根,则这三个实根的和为

2 若函数
若函数 的零点个数为
的零点个数为 ,则
,则 ______
______
3 一个高中研究性学习小组对本地区
一个高中研究性学习小组对本地区 年至
年至 年快餐公司发展情况进行了调查,制成了该地区快餐公司个数情况的条形图和快餐公司盒饭年销售量的平均数情况条形图(如图),根据图中提供的信息可以得出这三年中该地区每年平均销售盒饭 万盒
年快餐公司发展情况进行了调查,制成了该地区快餐公司个数情况的条形图和快餐公司盒饭年销售量的平均数情况条形图(如图),根据图中提供的信息可以得出这三年中该地区每年平均销售盒饭 万盒

4 函数
函数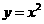 与函数
与函数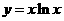 在区间
在区间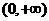 上增长较快的一个是
上增长较快的一个是

5 若
若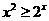 ,则
,则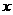 的取值范围是____________
的取值范围是____________
1 函数
函数 ( )
( )
A 是奇函数,且在
是奇函数,且在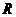 上是单调增函数
上是单调增函数
B 是奇函数,且在
是奇函数,且在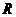 上是单调减函数
上是单调减函数
C 是偶函数,且在
是偶函数,且在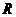 上是单调增函数
上是单调增函数
D 是偶函数,且在
是偶函数,且在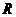 上是单调减函数
上是单调减函数
2 已知
已知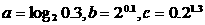 ,则
,则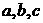 的大小关系是( )
的大小关系是( )
A
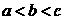 B
B
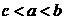
C
 D
D
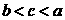
3 函数
函数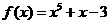 的实数解落在的区间是( )
的实数解落在的区间是( )
A
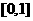 B
B
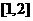 C
C
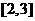 D
D

4 在
在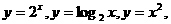 这三个函数中,当
这三个函数中,当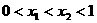 时,
时,
使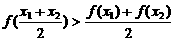 恒成立的函数的个数是( )
恒成立的函数的个数是( )
A
 个 B
个 B
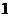 个 C
个 C
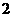 个 D
个 D
 个
个
5 若函数
若函数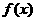 唯一的一个零点同时在区间
唯一的一个零点同时在区间 、
、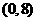 、
、 、
、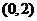 内,
内,
那么下列命题中正确的是( )
A 函数
函数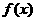 在区间
在区间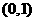 内有零点
内有零点
B 函数
函数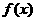 在区间
在区间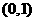 或
或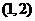 内有零点
内有零点
C 函数
函数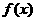 在区间
在区间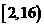 内无零点
内无零点
D 函数
函数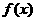 在区间
在区间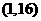 内无零点
内无零点
6 求
求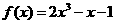 零点的个数为 ( )
零点的个数为 ( )
A
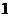 B
B
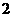 C
C
 D
D

7 若方程
若方程 在区间
在区间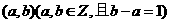 上有一根,则
上有一根,则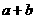 的值为( )
的值为( )
A
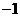 B
B
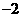 C
C
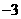 D
D

18、附加题:(不记总分)若函数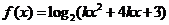 的定义域为R,求k的取值范围。
的定义域为R,求k的取值范围。
答案:DCBCB DAADD
11: 12:
12: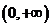 13:(1,2) 14:
13:(1,2) 14: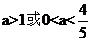
15: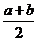
16: 奇函数
17:(1)
(2)减函数
18: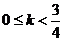
17、已知函数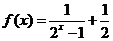
(1)求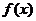 的定义域; (2)判断
的定义域; (2)判断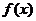 在区间
在区间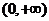 上的单调性,并证明。
上的单调性,并证明。
16、已知函数 ,判断
,判断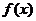 奇偶性。
奇偶性。
15、已知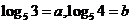 ,用
,用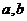 表示
表示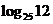 。
。
14、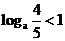 ,则a的取值范围是_________________________.
,则a的取值范围是_________________________.
13、函数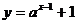
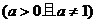 的图象必经过定点____________.
的图象必经过定点____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com