
题目列表(包括答案和解析)
5.若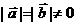 ,且
,且 ,
,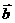 不共线,则
不共线,则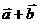 与
与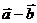 的关系是
( )
的关系是
( )
(A) 平行 (B) 垂直 (C) 相交但不垂直 (D) 相等
4.在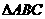 中,若
中,若 ,则
,则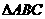 的形状一定是 ( )
的形状一定是 ( )
 A.等腰直角三角形 B.直角三角形 C.等腰三角形 D.等边三角形
A.等腰直角三角形 B.直角三角形 C.等腰三角形 D.等边三角形
3、直线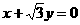 绕原点按顺时针方向旋转30°所得直线与圆
绕原点按顺时针方向旋转30°所得直线与圆 的位置
的位置
关系是 ( )
A、直线与圆相切 B、直线与圆相交但不过圆心 

C、直线与圆相离 D、直线过圆心
2、一个圆柱的内切球的半径为1,则圆柱与球的体积之比为 ( )
A、2
B、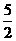 C、4
D、
C、4
D、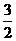
1、若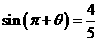 ,则
,则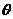 角的终边在
角的终边在
A.第一、二象限 B.第二、三象限 C.第一、四象限 D.第三、四象限
20.(本小题满分12分) (普通中学做) 在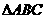 中,cosB=-
中,cosB=-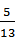 , cosC=
, cosC=
(I) 求 sinC的值;
(II)设BC=5,求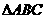 的面积.
的面积.
(示范性高中做)在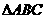 中,
中,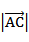 =2
=2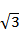 ,
,
 cosC+
cosC+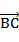 cosA=
cosA=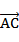 sinB
sinB
(I)求证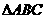 为等腰三角形;
为等腰三角形;
(II)求 ·
·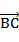 .的值.
.的值.
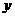
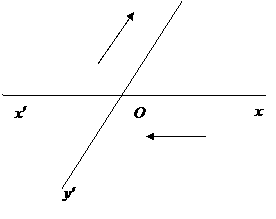 21. ( 本小题满分12分) .如图所示,有两条相交成
21. ( 本小题满分12分) .如图所示,有两条相交成 角的直路
角的直路 ,交点是
,交点是 ,甲、乙分别在
,甲、乙分别在 、
、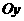 上,起初甲离
上,起初甲离 点3 km,乙离
点3 km,乙离 点1 km,后来两人同时用每小时4 km的速度,甲沿
点1 km,后来两人同时用每小时4 km的速度,甲沿 的方向,乙沿
的方向,乙沿 的方向步行.求:
的方向步行.求:
(Ⅰ)起初,两人的距离是多少?
(Ⅱ)用包含t的式子表示t小时后两人的距离.
(Ⅲ)什么时候两人的距离最短?
22 ( 本小题满分12分) (普通中学只做(Ⅰ)(Ⅱ),示范性高中全做)
已知向量a=(x-1,-1),b=(x-m,y),(m∈R),且a·b=0.
(Ⅰ)将y表示为x的函数y=f(x);
(Ⅱ)若tanA、tanB是方程f(x)+4=0的两个实根,A、B是锐角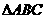 的两个内角,求证:m≥5;
的两个内角,求证:m≥5;
(Ⅲ)对任意实数α,恒有f(2+cosα)≤0,求证:m≥3.
19. (本小题满分12分)已知函数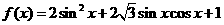 ,
,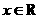 .求:
.求:
(I) 函数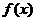 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(II) 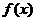 在
在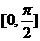 上的最值;
上的最值;
(Ⅲ)该函数的图像经过怎样的平移和伸缩变换可以得到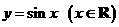 的图像?
的图像?
18.(本小题满分12分)平面内给定三个向量a=(3,2),b=(-1,2),c=(4,1),
(Ⅰ)求满足a=mb+nc的实数m、n;
(Ⅱ)若(a+kc)⊥(2b-a),求实数k.
17.(本小题满分10分)已知tan(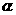 +
+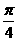 )=2,
)=2, 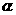 ∈(0,
∈(0, 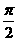 ).
).
. (Ⅰ)求tan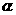 的值;
的值;
(Ⅱ)求sin(2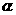 -
- )的值.
)的值.
16.下面有四个命题:
(1)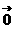 ·
·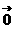 =
=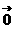 ;
(排版注意:这里带箭头的向量保持原样)
;
(排版注意:这里带箭头的向量保持原样)
(2)( ·
·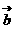 )·
)· =
= ·(
·(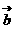 ·
· );
);
(3)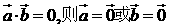 ;
;
(4)| ·
·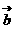 |.≤
|.≤ ·
·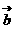
其中不正确命题的序号是_____________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com