4.若直线(2m²+m-3)x+(m²-m)y=4m-1在x轴上的截距为1，则实数m为(　　 )

A.1　　　 B.2　　　 C. 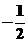　　　　D.2或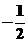

3．斜率为2的直线过(3,5)、(a,7)、(-1,b)，则a+b等于(　　 )

A.4　　　 B.-7　　　　 C.1　　　　 D.-1

2.点(1,3)、(5,7)和(10,12)的位置关系为(　　 )

A.同在一条直线上　　　　　　　　 B.三点间的距离两两相等

C.三点连线组成一个直角三角形　　 D. 三点连线组成一个等边三角形

1.过M(-2,m),N(m,4)的直线的倾斜角为90，则m的值为(　　 )

A.-2　　　 B.4　　　 C.2　　　　 D.-4

4.直线的方程：

(1)点斜式方程：_____________________________________________________,它适用于_______________________的直线.

(2)截距式方程：_____________________________________________________,它适用于_______________________的直线.

(3)两点式方程：_____________________________________________________,它适用于_______________________的直线.

(4)一般式方程：_____________________________________________________,它适用于_______________________的直线.

3．____________________________________叫做这条直线的倾斜角.垂直于x轴的直线的倾斜角为_________.直线的倾斜角的范围为______________.

2.经过两点A(x₁,y₁)、、B(x₂,y₂)的直线，当x₁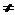x₂时，斜率k=_________,当___________时无斜率.

1．一般地，如果___________________________________,反之，______________________

__________________________________________,那么这个方程叫_________________,这条直线叫__________________.

2.解：点A为y=0与x－2y+1=0两直线的交点，

∴点A的坐标为(－1，0).

∴k_AB=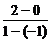=1.

又∵∠A的平分线所在直线的方程是y=0，

∴k _AC=－1.

∴直线AC的方程是y=－x－1.

而BC与x－2y+1=0垂直，∴k_BC=－2.

∴直线BC的方程是y－2=－2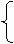(x－1).

y=－2x+4，

解得C(5，－6).

1.剖析：依据两直线位置关系判断方法便可解决.

解：当m=0时，l₁：x+6＝0，l₂：x＝0，

∴l₁∥l₂.

当m=2时，l₁：x+4y+6＝0，l₂：3y+2＝0，

∴l₁与l₂相交.

当m≠0且m≠2时，由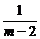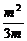＝得m=－1或m=3，由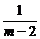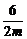＝得m＝3.

故(1)当m≠－1，m≠3且m≠0时，l₁与l₂相交；

(2)当m＝－1或m＝0时，l₁∥l₂；

(3)当m＝3时，l₁与l₂重合.