
题目列表(包括答案和解析)
7. 在正方体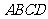 ―
―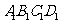 中,与
中,与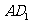 成60°角的面对角线共有( )
成60°角的面对角线共有( )
A.4条 B.6条 C.8条 D.10条
6. 已知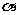 是第三象限角,则
是第三象限角,则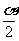 是( )
是( )
A. 第二象限角 B. 第一或第三象限角
C. 第四象限角 D. 第二或第四象限角
5. 设A是△ABC的一个内角,且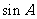 +
+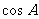 =
=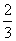 ,则这个三角形是( )
,则这个三角形是( )
A.锐角三角形 B.钝角三角形
C.非等腰的直角三角形 D.等腰直角三角形
4. 对于平面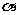 和共面的直线
和共面的直线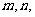 下列命题中真命题是( )
下列命题中真命题是( )
A.若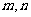 与
与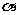 所成的角相等,则
所成的角相等,则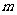 ∥
∥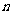 B.若
B.若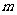 ∥
∥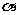 ,则
,则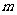 ∥
∥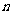
C.若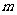 ⊥
⊥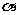 ,
,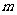 ⊥
⊥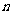 则
则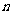 ∥
∥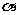 D.若
D.若 ,
,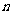 ∥
∥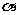 ,则
,则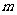 ∥
∥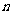
3. 若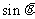 =
=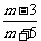 ,
,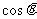 =
=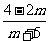 则m的值为( )
则m的值为( )
A. 0 B. 8 C .0或8 D. 3<m<9
2. 下列结论能成立的是( )
A.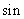
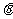 =
=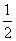 且
且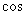
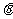 =
=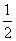 B. tan
B. tan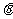 =2且
=2且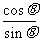 =
=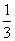
C. tan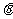 =1且
=1且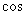
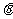 =
=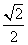 D.
D. 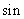
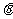 =1且
=1且 =
=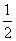
1. 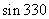 °等于( )
°等于( )
A.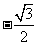 B.
B.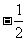 C.
C. 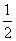 D.
D.
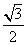
8、设每年付款x元,那么10年后
第一年付款的本利和为a1=1.0759x元。
第二年付款的本利和为a2=1.0758x元。
依次类推
第n年付款的本利和为an=1.07510-nx元。
则各年付款的本利和{an}为等比数列。
∴10年付款的本利和为S10=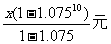 。
。
个人负担的余额总数为72×1000-28800-14400=28800元。
10年后余款的本利和为18800×1.07510
∴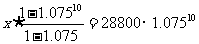 解得x=
解得x=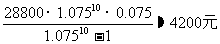
|

|
版权所有:()
版权所有:()
7、∵bn+1=bnq, ∴an+1an+2=anan+1q ∴an+2=anq,即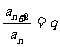
由a1=1,a3=q,a5=q2,……,知奇数项构成一个等比数列,故a2n-1=qn-1
由a2=r,a4=rq,a6=rq2,……,知偶数项也构成一个等比数列,故a2n=rqn-1
∴Cn=(1+r)qn-1
6.设an表示第n年年底扣除消费基金后的资金。
a1=1000(1+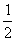 )-x
)-x
a2=[1000(1+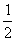 )-x](1+
)-x](1+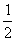 )-x=1000(1+
)-x=1000(1+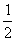 )2-x(1+
)2-x(1+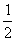 )-x
)-x
a3=[1000(1+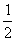 )2-x(1+
)2-x(1+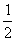 )-x](1+
)-x](1+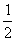 )-x=1000(1+
)-x=1000(1+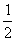 )3-x(1+
)3-x(1+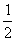 )2-x(1+
)2-x(1+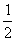 )-x
)-x
类推所得
a5=1000(1+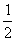 )5-x(1+
)5-x(1+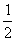 )4-x(1+
)4-x(1+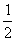 )3-x(1+
)3-x(1+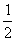 )2-x(1+
)2-x(1+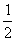 )-x
)-x
则1000(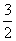 )5-x[(
)5-x[(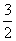 )4+(
)4+(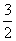 )3+…+1]=2000即1000(
)3+…+1]=2000即1000(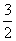 )5-x·
)5-x·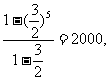
解得x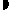 424万元
424万元
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com