3．已知两圆的半径分别为6和8，圆心距为14，则它们的公切线最多有(　　 )

A．1条　 B．2条　 C．3条　 D．4条

2．下列各式中运算正确的个数为(　　 )

①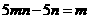；　 ②；　 ③；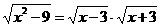

④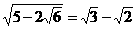

　 A．0个　 B．1个　 C．2个　 D．3个

1．在“”这8个实数中，有理数的个数为(　　 )

A．2个　 B．3个　 C．4个　 D．5个

22、(本小题满分14分)

对函数Φ(x)，定义f_k(x)＝Φ(x－mk)+nk(其中x∈(mk，m+mk]，k∈Z，m＞0，n＞0，且m、n为常数)为Φ(x)的第k阶阶梯函数，m叫做阶宽，n叫做阶高，已知阶宽为2，阶高为3. (1)当Φ(x)＝2^x时 　 ①求f₀(x)和f_k(x)的解析式； 　 ②求证：Φ(x)的各阶阶梯函数图象的最高点共线； (2)若Φ(x)＝x²，则是否存在正整数k，使得不等式f_k(x)＜(1－3k)x+4k²+3k－1有解？若存在，求出k的值；若不存在，请说明理由.

21、(本小题满分12分) 设直线l(斜率存在)交抛物线y²＝2px(p＞0，且p是常数)于两个不同点A(x₁，y₁)，B(x₂，y₂)，O为坐标原点，且满足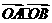＝x₁x₂+2(y₁+y₂). (1)求证：直线l过定点； (2)设(1)中的定点为P，若点M在射线PA上，满足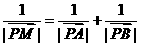，求点M的轨迹方程.

20、(本小题满分12分) 已知等差数列{a_n²}中，首项a₁²＝1，公差d＝1，a_n＞0，n∈N^*. (1)求数列{a_n}的通项公式； (2)设b_n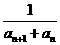＝，数列{b_n}的前n项和为T_n；　

　 ①求T₁₂₀； 　 ②求证：当n＞3时，2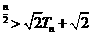

19、(本小题满分12分) 如图，在四边形ABCD中，AC⊥BD，垂足为O，PO⊥平面ABCD，AO＝BO＝DO＝1，CO＝PO＝2，E是线段PA上的点，AE∶AP＝1∶3. (1)求证：OE∥平面PBC；　

(2)求二面角D－PB－C的大小

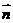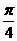18、(本小题满分12分) 已知向量＝(sin2x，cos2x)，＝(cos，sin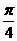)，函数f(x)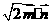＝+2a(其中a为实常数) (1)求函数f(x)的最小正周期； (2)若x∈[0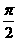，]时，函数f(x)的最小值为－2，求a的值.

17、某公司购买了一博览会门票10张，其中甲类票4张，乙类票6张，现从这10张票中任取3张奖励一名员工. (1)求该员工得到甲类票2张，乙类票1张的概率； (2)求该员工得到甲类票张数多于乙类票张数的概率，

(本小题满分12分)

14、