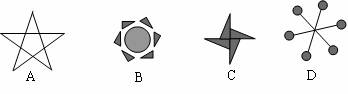
2．如图所示，既是轴对称图形又是中心对称图形的是(　　 )

1． 举世瞩目的三峡大坝于2006年5月20日胜利封顶。坝体混凝土浇筑量约为2643万m³，将这一数据用科学记数法表示为

A、2．643×10³m³　　　 B、0．2643×10⁸m³　　 C、26．43×10⁶m³　　 D、2．643×10⁷m³

25．(13分)我市某乡A，B两村盛产柑桔，A村有柑桔200吨，B村有柑桔300吨．现将这些柑桔运到C，D两个冷藏仓库，已知C仓库可储存240吨，D仓库可储存260吨；从A村运往C，D两处的费用分别为每吨20元和25元，从B村运往C，D两处的费用分别为每吨15元和18元。设从A村运往C仓库的柑桔重量为吨，A、B两村运往两仓库的柑桔运输费用分别为元和元．

(1)请填写下表，并求出、与之间的函数关系式；

解：

收地 货运	C	D	总计
A	吨		200吨
B			300吨
总计	240吨	260吨	500吨

(2)试讨论A，B两村中，哪个村的运费较少；

(3)考虑到B村的经济承受能力，B村的柑桔运费不得超过4830元．在这种情况下，请问怎样调运，才能使两村运费之和最小?求出这个最小值。

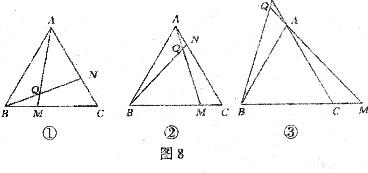
24．(12分)△ABC为正三角形(即AB=AC=BC；∠A=∠B=∠C=60°)，点M是射线BC上任意一点，点N是射线CA上任意一点，且BM=CN，直线BN与AM相交于Q点，就下面给出的三种情况，如图8中的①②③，先用量角器分别测量∠BQM的大小，然后猜测∠BQM等于多少度．并利用图③证明你的结论。

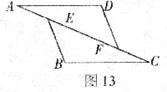
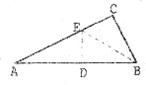
23．(10分)如图13，在△AFD和△CEB中，点A、E、F、C在同一直线上，有下面四个论断：(1)AD=CB，(2)AE=CF，(3)∠B=∠D，(4)AD//BC．请用其中三个作为条件，余下一个作为结论，编一道数学问题，并写出解答过程．

22．(10分)如图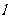，₁反映了甲离开A的时间与离A地的距离的关系，₂反映了乙离开A地的时间与离A地的距离之间的关系，根据图象填空：

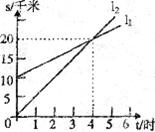
(1)当时间为2小时时，甲离A地________千米，乙离A地________千米。

(2)当时间为6小时时，甲离A地_________米。乙离A地________千米。

(3)当时间________时，甲、乙两人离A地距离相等。

(4)当时间________时，甲在乙的前面，当时间_______时，乙超过了甲。

(5) ₁对应的函数表达式为______________，₂对应的函数表达式为______________。

21．(10分)为了了解某初中学生的体能情况，抽取若干名学生在单位时间内进行引体向上测试，将所得数据整理后，画出频数分布直方图(如图4)，图中从左到右依次为第1、2、3、4、5组。

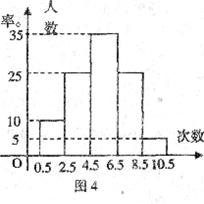
(1)　 求抽取多少名学生参加测试?

(2)　 处于哪个次数段的学生数最多?(答出是第几组即可)

(3)　 若次数在5次(含5次)以上为达标，求这次测试的达标率。

20．如图把Rt△ABC(∠C=90°)折叠，使A、B两点重合，得到折ED，再沿BE折叠，C点恰好与D点重合，则∠A等于______________度．

19．小强调查“每人每天的用水量”这一问题时，收集到80个数据，最大数据是70升，最小数据是42升，若取组距为4，则应分为______________组绘制频数分布表．

18．已知直线与坐标轴围成的三角形面积是，则此直线的函数解析式是__________．