
3.如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面,与“迎”相对的面上的汉字是( )
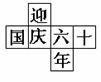
A.国 B.庆 C.六 D.年
2.温家宝总理有一句名言:“多么小的问题,乘以13亿,都会变得很大,多么大的经济总量,除以13亿,都会变得很小”. 如果每人每天浪费0.01千克粮食,我国13亿人每天就浪费粮食( )
A.1.3×105 千克 B.1.3×106千克 C.1.3×107千克 D.1.3×108千克
在每个小题给出的四个备选答案中,只有一个是正确的,请将所选答案前的字母按规定要求填涂在“答题卡”第1-8题的相应位置上.
1.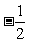 的倒数是(
)
的倒数是(
)
A.-2 B.2 C.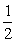 D.
D.
25.已知抛物线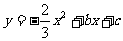 与x轴交于不同的两点
与x轴交于不同的两点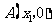 和
和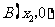 ,与y轴交于点C,且
,与y轴交于点C,且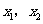 是方程
是方程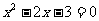 的两个根(
的两个根(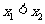 ).
).
(1)求抛物线的解析式;
(2)过点A作AD∥CB交抛物线于点D,求四边形ACBD的面积;
(3)如果P是线段AC上的一个动点(不与点A、C重合),过点P作平行于x轴的直线l交BC于点Q,那么在x轴上是否存在点R,使得△PQR为等腰直角三角形?若存在,求出点R的坐标;若不存在,请说明理由.
24.如图,在平面直角坐标系中,直线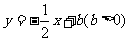 分别交
分别交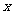 轴、
轴、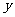 轴于
轴于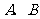 两点.点
两点.点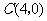 、
、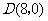 ,以
,以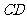 为一边在
为一边在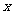 轴上方作矩形
轴上方作矩形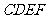 ,且
,且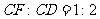 .设矩形
.设矩形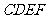 与
与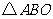 重叠部分的面积为
重叠部分的面积为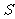 .
.
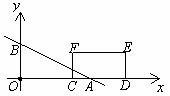
(1)求点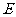 、
、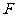 的坐标;
的坐标;
(2)当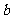 值由小到大变化时,求
值由小到大变化时,求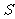 与
与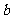 的函数关系式;
的函数关系式;
(3)若在直线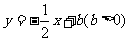 上存在点
上存在点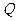 ,使
,使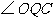 等于
等于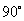 ,请直接写出
,请直接写出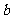 的取值范围.
的取值范围.
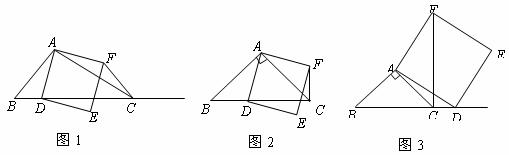
23.如图1,在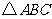 中,
中,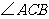 为锐角,点
为锐角,点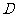 为射线
为射线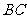 上一点,联结
上一点,联结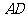 ,以
,以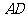 为一边且在
为一边且在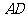 的右侧作正方形
的右侧作正方形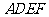 .
.
(1)如果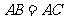 ,
,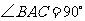 ,
,
①当点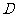 在线段
在线段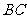 上时(与点
上时(与点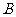 不重合),如图2,线段
不重合),如图2,线段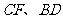 所在直线的位置关系为 __________ ,线段
所在直线的位置关系为 __________ ,线段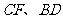 的数量关系为
;
的数量关系为
;
②当点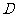 在线段
在线段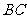 的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果 ,
,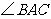 是锐角,点
是锐角,点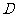 在线段
在线段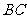 上,当
上,当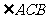 满足什么条件时,
满足什么条件时,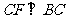 (点
(点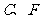 不重合),并说明理由.
不重合),并说明理由.
22.(本小题满分5分)
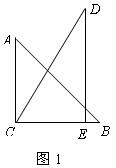
把两个三角形按如图1放置,其中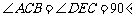 ,
,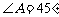 ,
,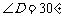 ,且
,且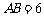 ,
,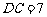 .把△DCE绕点C顺时针旋转15°得到△D1CE1,如图2,这时AB与CD1相交于点
.把△DCE绕点C顺时针旋转15°得到△D1CE1,如图2,这时AB与CD1相交于点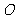 ,与D1E1相交于点F.
,与D1E1相交于点F.
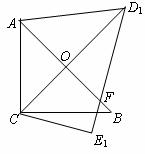
(1)求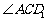 的度数;
的度数;
(2)求线段AD1的长;
(3)若把△D1CE1绕点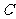 顺时针再旋转30°得到△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?请说明理由.
顺时针再旋转30°得到△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?请说明理由.
21.(本小题满分5分)
列方程或方程组解应用题:
2008年5月12日14时28分在我国四川省汶川地区发生了里氏8.0级强烈地震,灾情牵动全国人民的心.“一方有难、八方支援”,某厂计划加工1500顶帐篷支援灾区,在加工了300顶帐篷后,由于情况紧急,该厂又增加了人员进行生产,将工作效率提高到原来的1.5倍,结果提前4天完成任务.问该厂原来每天加工多少顶帐篷.
20.某校学生会准备调查本校初中三年级同学每天(除课间操外)课外锻炼的平均时间.
(1)确定调查方式时,①甲同学说:“我到1班去调查全体同学”;②乙同学说:“我到体育场上去询问参加锻炼的同学”;③丙同学说:“我到初中三年级每个班去随机调查一定数量的同学”.上面同学说的三种调查方式中最为合理的是___________(填写序号);
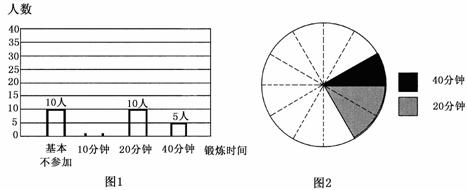
(2)他们采用了最为合理的调查方式收集数据,并绘制出如图1所示的条形统计图和如图2所示的扇形统计图,请将图1补充完整;
(3)若该校初中三年级共有240名同学,则其中每天(除课间操外)课外锻炼平均时间不大于20分钟的人数约为__________人.
(注:图2中相邻两虚线形成的圆心角为30°)
19.(本小题满分5分)
如图,点D是⊙O直径CA的延长线上一点,点B在⊙O上,且AB=AD=AO.
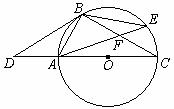
(1)求证:BD是⊙O的切线;
(2)若点E是劣弧BC上一点,弦AE与BC相交于点F,且CF=9,cos∠BFA=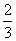 ,求EF的长.
,求EF的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com