
2.在函数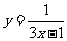 中,自变量
中,自变量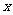 的取值范围是
的取值范围是
A.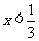 B.
B. 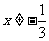 C.
C. 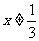 D.
D. 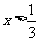
1.计算2×(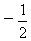 )的结果是
)的结果是
A.一1 B.l C.一2 D.2
26、(12分)已知二次函数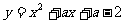 。
。
(1)求证:不论a为何实数,此函数图象与x轴总有两个交点。
(2)设a<0,当此函数图象与x轴的两个交点的距离为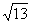 时,求出此二次函数的解析式。
时,求出此二次函数的解析式。
(3)若此二次函数图象与x轴交于A、B两点,在函数图象上是否存在点P,使得△PAB的面积为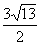 ,若存在求出P点坐标,若不存在请说明理由。
,若存在求出P点坐标,若不存在请说明理由。
25、(12分)凯里市某大型酒店有包房100间,在每天晚餐营业时间,每间包房收包房费100元时,包房便可全部租出;若每间包房收费提高20元,则减少10间包房租出,若每间包房收费再提高20元,则再减少10间包房租出,以每次提高20元的这种方法变化下去。
(1)设每间包房收费提高x(元),则每间包房的收入为y1(元),但会减少y2间包房租出,请分别写出y1、y2与x之间的函数关系式。
(2)为了投资少而利润大,每间包房提高x(元)后,设酒店老板每天晚餐包房总收入为y(元),请写出y与x之间的函数关系式,求出每间包房每天晚餐应提高多少元可获得最大包房费收入,并说明理由。
24、(12分)如图,l1、l2、l3、l4是同一平面内的四条平行直线,且每相邻的两条平行直线间的距离为h,正方形ABCD的四个顶点分别在这四条直线上,且正方形ABCD的面积是25。
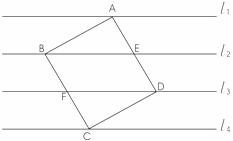
(1)连结EF,证明△ABE、△FBE、△EDF、△CDF的面积相等。
(2)求h的值。
23、(10分)赏郎中学初三某班的同学积极参加体育锻炼,该班班长在篮球场对自己进行篮球定点投球测试,下表是他的测试成绩及相关数据:
|
|
第一回投球 |
第二回投球 |
第三回投球 |
第四回投球 |
第五回投球 |
第六回投球 |
|
每回投球次数 |
5 |
10 |
15 |
20 |
25 |
30 |
|
每回进球次数 |
3 |
8 |
|
16 |
17 |
18 |
|
相应频率 |
0.6 |
0.8 |
0.4 |
0.8 |
0.68 |
0.6 |
(1)请将数据表补充完整。
(2)画出班长进球次数的频率分布折线图。
(3)就数据5、10、15、20、25、30而言,这组数据的中位数是多少?
(4)如果这个测试继续进行下去,每回的投球次数不断增加,根据上表数据,测试的频率将稳定在他投球1次时进球的概率附近,请你估计这个概率是多少?并说明理由。(结果用分数表示)
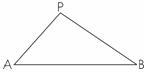
22、(9分)如图,在凯里市某广场上空飘着一只汽球P,A、B是地面上相距90米的两点,它们分别在汽球的正西和正东,测得仰角∠PAB=45o,仰角∠PBA=30o,求汽球P的高度(精确到0.1米,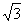 =1.732)
=1.732)
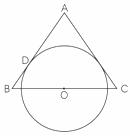
21、(9分)如图,△ABC为等腰三角形,AB=AC,O是底边BC的中点,⊙O与腰AB相切于点D,求证AC与⊙O相切。
20、(7分)若不等式组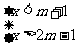 无解,求m的取值范围。
无解,求m的取值范围。
19、(7分)先化简,再求值: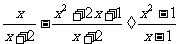 ,其中
,其中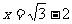 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com