
8、设矩形ABCD的长与宽的和为2,以AB为轴心旋转一周得到一个几何体,则此几何体的侧面积有( )
A.最小值4π B.最大值4π
C.最大值2π D.最小值2π
7、方程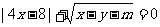 ,当
,当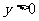 时,m的取值范围是( )
时,m的取值范围是( )
A.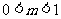 B.
B.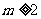
C.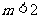 D.
D.
6、如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )
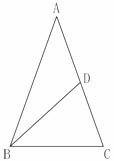
A.30o B.40o C.45o D.36o
5、抛物线的图象如图所示,根据图象可知,抛物线的解析式可能是( )
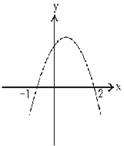
A.y=x2-x-2
B.y=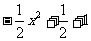
C.y=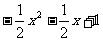 D.y=
D.y=
4、下面简举几何体的主视图是( )

正面 A B C D
3、下列图形中,面积最大的是( )
A.对角线长为6和8的菱形; B.边长为6的正三角形;
C.半径为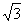 的圆;
D.边长分别为6、8、10的三角形;
的圆;
D.边长分别为6、8、10的三角形;
2、在下列几何图形中一定是轴对称图形的有( )

A.1个 B.2个 C.3个 D.4个
1、下列运算正确的是( )
A.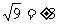 B.
B.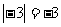 C.
C.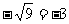 D.
D.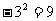
25.如图1,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
解答下列问题:
(1)如果AB=AC,∠BAC=90º.
①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD之间的位置关系为 ,数量关系为 .
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,为什么?
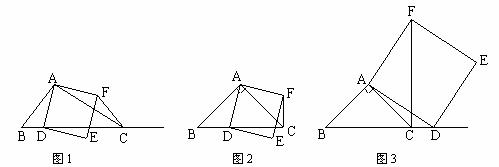
(2)①如果AB=AC,∠BAC≠90º,点D在射线BC上运动.在图4中同样作出正方形ADEF,你发现(1)问中的结论是否成立?不用说明理由;
②如果∠BAC=90º,AB≠AC,点D在射线BC上运动.在图5中同样作出正方形ADEF,你发现(1)问中的结论是否成立?不用说明理由;
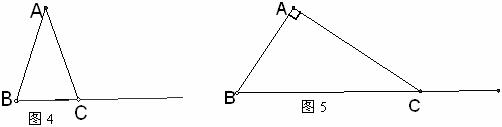
(3)要使(1)问中CF⊥BC的结论成立,试探究:△ABC应满足的一个条件,(点C、F重合除外)?画出相应图形(画图不写作法),并说明理由;
(4)在(3)问的条件下,设正方形ADEF的边DE与线段CF相交于点P,
设AC=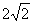 ,BC=
,BC=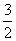 ,求线段CP长的最大值.
,求线段CP长的最大值.
24.把直线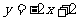 沿x轴翻折恰好与抛物线
沿x轴翻折恰好与抛物线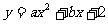 交于点C(1,0)和点A(8,m),.
交于点C(1,0)和点A(8,m),.
(1)求该抛物线的解析式;
(2)设该抛物线与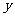 轴相交于点
轴相交于点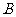 ,设点
,设点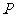 是
是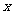 轴上的任意一点(点
轴上的任意一点(点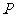 与点
与点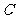 不重合),若
不重合),若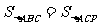 ,求满足条件的
,求满足条件的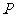 点的坐标;
点的坐标;
(3)设点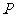 是
是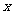 轴上的任意一点,试判断:
轴上的任意一点,试判断: 与
与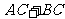 的大小关系,并说明理由.
的大小关系,并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com