
4.在反比例函数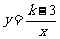 图象的每一支曲线上,
图象的每一支曲线上,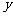 都随
都随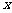 的增大而减小,则
的增大而减小,则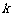 的取值范围是( ).
的取值范围是( ).
A.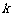 >3 B.
>3 B.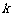 >0 C.
>0 C.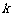 <3 D.
<3 D.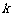 <0
<0
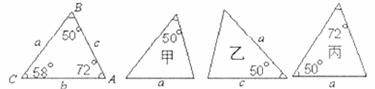
3.如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形能与△ABC全等的图形是( ).
A.甲乙 B.甲丙 C.乙丙 D.乙
2.函数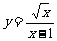 的自变量
的自变量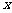 的取值范围是( )
的取值范围是( )
A.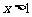 B.
B.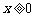 C.
C.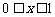 D.
D.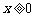 且
且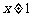
1.在平面直角坐标系中,下列各点位于第四象限的是( )
A.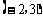 B.
B.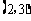 C.
C.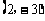 D.
D.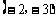
23.(本题满分12分)
如下图1,在平面直角坐标系中,已知点A(0,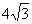 ),点B在
),点B在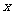 正半轴上,且∠ABO=30°。动点P在线段AB上从点A向点B以每秒
正半轴上,且∠ABO=30°。动点P在线段AB上从点A向点B以每秒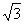 个单位的速度运动,设运动时间为
个单位的速度运动,设运动时间为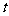 秒。在
秒。在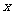 轴上取两点M,N作等边△PMN。
轴上取两点M,N作等边△PMN。
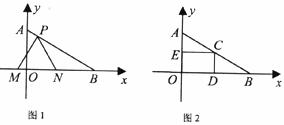
(1)求直线AB的解析式;
(2)求等边△PMN的边长(用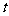 的代数式表示),并求出当等边△PMN的顶点M运动到与原点O重合时
的代数式表示),并求出当等边△PMN的顶点M运动到与原点O重合时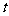 的值;
的值;
(3)如果取OB的中点D,以OD为边在Rt△AOB内部作如上图2所示的矩形ODCE,点C在线段AB上。设等边△PMN和矩形ODCE重叠部分的面积为S,请求出当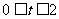 0秒时S与
0秒时S与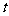 的函数关系式,并求出S的最大值。
的函数关系式,并求出S的最大值。
22.(本题满分10分)
如图,已知⊙O1与⊙O2相切于点P,它们的半径分别为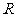 、
、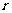 ,一直线绕P点旋转与⊙O1、⊙O2分别交于点A、B(点P、B不重合),探索规律:
,一直线绕P点旋转与⊙O1、⊙O2分别交于点A、B(点P、B不重合),探索规律:
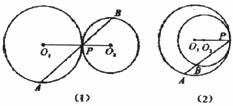
(1)如上图1,当⊙O1与⊙O2外切时。探索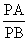 与半径
与半径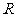 、
、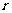 之间的关系式,请证明你的结论;
之间的关系式,请证明你的结论;
(2)如上图2,当⊙O1与⊙O2内切时,第(1)题探求的结论是否成立?为什么?
21.(本题满分10分)
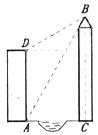
如下图,小丽的家住在某一河畔的电梯公寓AD内,她家的河对岸新建了一座大厦BC。为了测得大厦的高度,小丽在她家的楼底A处测得大厦顶部B的仰角为60°,爬上楼顶D处测得大厦的顶部B的仰角为30°。已知小丽所住的电梯公寓高82米,请你帮助小丽计算出大厦高度BC及大厦与小丽所住电梯公寓间的距离AC。(计算结果保留根号)
20.(本题满分10分)
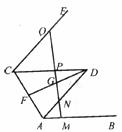
如下图,AB∥CD、AD∥CE,F、G分别是AC和FD的中点,过G的直线依次交AB、AD、CD、CE于点M、N、P、Q,求证:MN+PQ=2PN。
19.(本题满分8分)
某省为解决农村饮用水问题,省财政部门共投资20亿元对各市的农村饮用水的 “改水工程”予以一定比例的补助。2008年,A市在省财政补助的基础上投入600万元用于“改水工程”,计划以后每年以相同的增长率投资,2010年该市计划投资“改水工程”1176万元。
(1)求A市投资“改水工程”的年平均增长率;
(2)从2008年到2010年,A市三年共投资“改水工程”多少万元?
18.(本题满分8分)
2008年北京奥运会刚刚过去,2012年伦敦奥运会已在向世人招手。某校学生会为了了解全校同学最想收看伦敦奥运会哪种比赛项目的情况。随机调查了200名同学,根据调查结果制作了如下频数分布表:
|
最想收看的项目 |
频数(人数) |
频率 |
|
足球 |
|
0.14 |
|
篮球 |
36 |
0.18 |
|
排球 |
16 |
0.08 |
|
羽毛球 |
30 |
0.15 |
|
乒乓球 |
|
|
|
游泳 |
16 |
0.08 |
|
跳水 |
20 |
0.10 |
|
田径 |
4 |
0.02 |
|
合计 |
200 |
|
(1)补全频数分布表;
(2)指出这个问题中的个体、总体、样本和样本容量;
(3)在这次抽样调查中,最想收看哪个奥运会比赛项目的同学最多?最想收看哪个比赛项目的同学最少?
(4)根据以上调查,试估计该校5100名学生中,最想收看游泳比赛的人数。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com