
4.对于反比例函数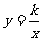 ,当
,当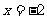 时,
时,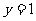 ,则
,则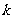 的值为
的值为
A. -2 B.2 C.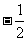 D.
D.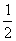
3.纳米是一种长度单位,1纳米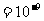 米,已知某种花粉的直径为3500纳米,那么用科学记数法表示该种花粉的直径为
米,已知某种花粉的直径为3500纳米,那么用科学记数法表示该种花粉的直径为
A.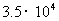 米 B.
米 B.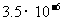 米 C.
米 C.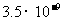 米 D.
米 D.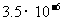 米
米
2.△ABC的三条边长分别是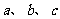 ,则下列各式成立的是
,则下列各式成立的是
A.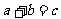 B.
B.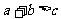 C.
C.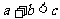 D.
D.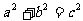
1.分式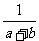 ,
,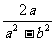 ,
,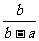 的最简公分母为
的最简公分母为
A.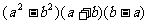 B.
B.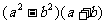
C.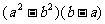 D.
D.
25.(本题满分l l分)一家化工厂原来每月利润为l20万元.从今年一月起安装使用回收净化设备(安装时间不计),一方面改善了环境,另一方面大大降低原料成本.据测算,使用回收净化设备后的l至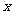 月(1≤
月(1≤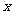 ≤12)的利润的月平均值
≤12)的利润的月平均值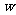 (万元)满足
(万元)满足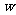 =l0x+90,第2年的月利润稳定在第1年的第l2个月的水平。
=l0x+90,第2年的月利润稳定在第1年的第l2个月的水平。
(1)设使用回收净化设备后的1至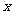 月(1≤
月(1≤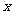 ≤12)的利润和为y,写出
≤12)的利润和为y,写出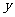 关于
关于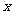 的函数关系式,并求前几个月的利润和等于700万元?
的函数关系式,并求前几个月的利润和等于700万元?
(2)当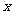 为何值时,使用回收净化设备后的1至
为何值时,使用回收净化设备后的1至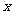 月的利润和与不安装回收净化设备时
月的利润和与不安装回收净化设备时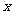 个月的利润和相等?
个月的利润和相等?
(3)求使用回收净化设备后两年的利润总和。
24.(本题满8分)将正六边形纸片按下列要求分割(每次分割,纸片均不得有剩余);
第一次分割:将正六边形纸片分割成三个全等的菱形,然后选取其中的一个菱形再分割成一个正六边形和两个全等的正三角形;
第二次分割:将第一次分割后所得的正六边形纸片分割成三个全等的菱形,然后选取其中的一个菱形再分割成一个正六边形和两个全等的正三角形;按上述分割方法进行下去……
(1)请你在下图中画出第一次分割的示意图;
(2)若原正六边形的面积为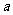 ,请你通过操作和观察,将第l次,第2次,第3次分割后所得的正六边形的面积填入下表:
,请你通过操作和观察,将第l次,第2次,第3次分割后所得的正六边形的面积填入下表:
|
分割次数(n) |
1 |
2 |
3 |
… |
|
正六边形的面积s |
|
|
|
|
(3)观察所填表格,并结合操作,请你猜想:分割后所得的正六边形的面积S与分割次数,n有何关系?(s用含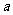 和n的代数式表示,不需要写出推理过程)
和n的代数式表示,不需要写出推理过程)
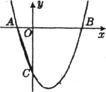
23.(本题满分l3分)抛物线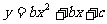 与
与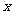 轴交于A(一1,0)、B(3,0)两点。
轴交于A(一1,0)、B(3,0)两点。
(1)求该抛物线的解析式:
(2)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足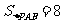 ,并求出此时P点的坐标;
,并求出此时P点的坐标;
(3)设(1)中的抛物线交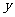 轴于C点,在该抛物线的对称轴上是否存在点Q,使得
轴于C点,在该抛物线的对称轴上是否存在点Q,使得 QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
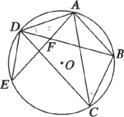
22.(本题满分7分)如图, ABC内接于⊙O,过C作CD∥AB与⊙O相交于D点,E是
ABC内接于⊙O,过C作CD∥AB与⊙O相交于D点,E是 上一点,且满足AD=DE连接BD与AE相交于点F
上一点,且满足AD=DE连接BD与AE相交于点F
求证:△ADF∽△ABC
21.(本题满分9分)项王故里的门票价格规定如下表:
|
购票人数 每人门票价 |
1-50人 5元 |
51一l00人 4.5元 |
100人以上 4元 |
某校九年级甲、乙两个班共有103人(其中甲班人数多于乙班人数)去游项王故里,如果两班都以班为单位分别购票,则一共需486元.
(1)如两班联合起来作为一个团体购票,则可以节约多少元钱?
(2)两班各有多少名学生?
20.(本题满分8分)如图,EG∥AF,请你从下面三个条件中,再选两个作已知条件,另一个为结论,推出一个正确的命题(只需写出一种情况)
①AB=AC ②DE=DF ③BE=CF
已知:EG∥AF,____________=________________,_____________=_______________。
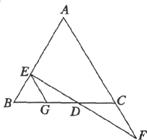
求证:
证明:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com