
7.如图是由几个相同的小正方体搭成几何体的三视图,则搭成这个几何体的小正方体的个数是 ( )
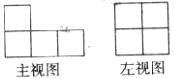
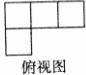
A.4个 B.5个 C.6个 D.7个
6.数学课上,老师要同学们判断一个四边形门框是否为矩形.下面是某合作小组的4位同学拟定的方案,其中正确的是 ( )
A.测量对角线是否互相平分 B.测量两组对边是否分别相等
C.测量一组对角是否都为直角 D.测量三个角是否为直角
5.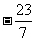 ,3
,3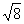 ,
, ,sin60°中无理数的个数是 ( )
,sin60°中无理数的个数是 ( )
A.1个 B.2个 C.3个 D.4个
4.5月4日青年节,学生会组织的游园晚会中有一个闯关活动:将5张分别画有等腰梯形、圆、平行四边形、等腰三角形、菱形的卡片任意摆放,有图形的一面向下,从中任意翻开一张,如果是轴对称图形就可过关.那么,一次过关的概率是 ( )
A.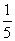 B.
B.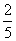 C.
C.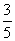 D.
D.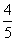
3.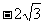 与
与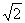 之间最小的整数是 ( )
之间最小的整数是 ( )
A.0 B.-l C.-2 D.-3
2.为应对全球金融危机,我国采取宽松信贷货币政策,今年三月份我国信贷激增1.89万亿,将这个数用科学记数法表示出来为 ( )
A.1.89×108 B.1.89×1012 C.1.89×1013 D.1.89×1011
1.我们把零上16°记作+16℃,则零下2℃可记作 ( )
A.+2 B.-2 C.2℃ D.-2℃
25.(本小题满分12分)
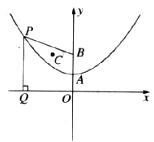
如图,抛物线的顶点A的坐标(0,2),对称轴为y轴,且经过点(-4,4).
(1)求该抛物线的表达式.
(2)若点B的坐标为(0,4),P为抛物线上一点(如图),过点P作.PQ⊥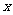 轴于点Q,连接PB,求证:PQ=PB.
轴于点Q,连接PB,求证:PQ=PB.
(3)若点C(-2,4),利用(2)的结论,判断抛物线上是否存在一点K,使△KBC的周长最小,若存在,求出这个最小值,并求此时点K的坐标;若不存在,请说明理由。
24.(本小题满分l0分)
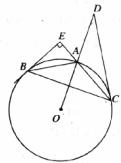
如图,△ABC内接于⊙O,过点B的切线与CA的延长线相交于点E,且∠BEC=90°,点D在OA的延长线上,AO⊥BC,∠ODC=30°.
(1)求证:DC为⊙O的切线.
(2)若CA=6,求DC的长.
23.(本小题满分9分)
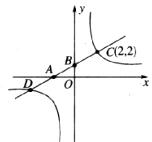
如图,一次函数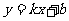 的图象与反比例函数
的图象与反比例函数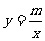 的图象相交于点C(2,2),与
的图象相交于点C(2,2),与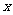 轴负半轴交于点A,与
轴负半轴交于点A,与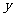 轴交于点B,O为坐标原点,且tan∠BAO=
轴交于点B,O为坐标原点,且tan∠BAO=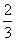 .
.
(1)求反比例函数与一次函数的表达式.
(2)求一次函数与反比例函数图象的另一交点D的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com