
8.袋中有5个球,3个新球,2个旧球,每次取一个,无放回抽取2次,则第2次抽到新球的概率是( )
A.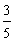 B.
B.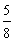 C.
C.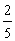 D.
D.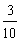
7.甲、乙两人进行围棋比赛,比赛采取五局三胜制,无论哪一方先胜三局则比赛结束,假定甲每局比赛获胜的概率均为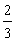 ,则甲以3∶1的比分获胜的概率为( )
,则甲以3∶1的比分获胜的概率为( )
A.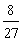 B.
B.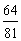 C.
C.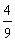 D.
D.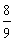
6.以A={2,4,6,7,8,11,12,13}中的任意两个元素分别为分子与分母构成分数,则这种分数是可约分数的概率是( )
A.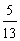 B.
B.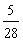 C.
C.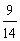 D.
D.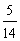
5.袋中装有6个白球,5只黄球,4个红球,从中任取1球,抽到的不是白球的概率为( )
A.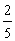 B.
B.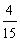 C.
C.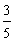 D.非以上答案
D.非以上答案
4.在两个袋内,分别写着装有0,1,2,3,4,5六个数字的6张卡片,今从每个袋中各任取一张卡片,则两数之和等于5的概率为( )
A.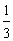 B.
B.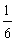 C.
C.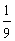 D.
D.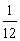
3.从1,2,3,4这4个数中,不放回地任意取两个数,两个数都是偶数的概率是( )
A.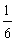 B.
B.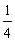 C.
C.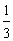 D.
D.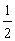
2.从甲,乙,丙三人中任选两名代表,甲被选中的的概率是( )
A.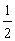 B.
B.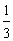 C.
C.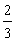 D.1
D.1
1. 从装有2个红球和2个白球的口袋中任取2个球,那么互斥而不对立的两个事件是( )
A.至少有一个白球和全是白球 B.至少有一个白球和至少有一个红球
C.恰有一个白球和恰有2个白球 D.至少有一个白球和全是红球
21.(本小题满分12分)
已知向量p=(-cos2x,a),q=(a,2-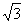 sin2x),函数f(x)=p·q-5(a∈R,a≠0).
sin2x),函数f(x)=p·q-5(a∈R,a≠0).
(1)求函数f(x)(x∈R)的值域;
(2)a=2时,若对任意的t∈R,函数y=f(x),x∈(t,t+b]的图象与直线y=一l有且仅有两个不同的交点,试确定b的值(不必证明),并求函数y=f(x)在[0,b]上的单调递增区间.
20.(本小题满分l2分)
一只口袋内装有形状、大小都相同的6只小球,其中4只白球,2只红球,从袋中随机摸出2只球.
(1)求2只球都是红球的概率;
(2)求至少有l只球是红球的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com