
3.下列各数中最大的数是
A.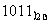 B.
B.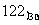 C.
C.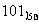 D.
D.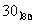
2.复数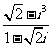 等于
等于
A.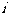 B.
B. C.
C.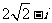 D.
D.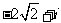
1.用反证法证明命题“若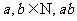 可被
可被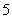 整除,那么
整除,那么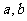 中至少有一个能被
中至少有一个能被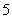 整除”.那么假设的内容是
整除”.那么假设的内容是
A.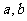 都能被
都能被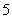 整除
B.
整除
B.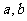 都不能被
都不能被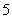 整除
整除
C.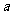
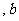 有一个能被
有一个能被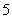 整除 D.
整除 D.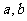 有一个不能被
有一个不能被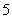 整除
整除
9.若把满足二元二次不等式(组)的平面区域叫做二次平面域.
(1)画出9x2-16y2+144≤0对应的二次平面域;
(2)求x2+y2的最小值;
(3)求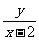 的取值范围.
的取值范围.
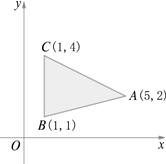
8.给出的平面区域是△ABC内部及边界(如下图),若目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,求a的值及z的最大值.
7.已知-4≤a-b≤-1,-1≤4a-b≤5,求9a-b的取值范围.
6.一个农民有田2亩,根据他的经验,若种水稻,则每亩每期产量为400千克;若种花生,则每亩每期产量为100千克,但水稻成本较高,每亩每期需240元,而花生只要80元,且花生每千克可卖5元,稻米每千克只卖3元,现在他只能凑足400元,问这位农民对两种作
物各种多少亩,才能得到最大利润?
5.画出不等式组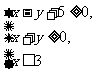 表示的平面区域.
表示的平面区域.
4.甲、乙两地生产某种产品,它们可调出的数量分别是300t和750t.A.B.C三地需要该种产品的数量分别为200t、450t、400t,甲运往A.B.C三地每1t产品的运费分别为6元、3元、5元,乙地运往A.B.C三地每1t产品的运费分别为5元、9元、6元,为使运费最低,调运方案是_______,最低运费是_______.
3.用不等式组表示以点(0,0)、(2,0)、(0,-2)为顶点的三角形内部,该不等式组为_______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com