
2.设复数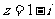 ,则复数
,则复数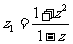 在复平面内所对应的点在 ( )
在复平面内所对应的点在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
1.与直线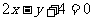 平行的抛物线
平行的抛物线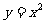 的切线方程为 ( )
的切线方程为 ( )
A.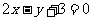 B.
B.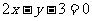 C.
C.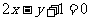 D.
D.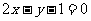
21.(本小题满分12分)
已知定义在R上奇函数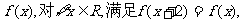 且当
且当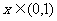 时,
时,
|
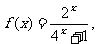
(Ⅰ)求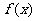 在[-1,1]上的解析式;
在[-1,1]上的解析式;
(Ⅱ)证明: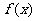 在(0,1)上是减函数.
在(0,1)上是减函数.
20.(本小题满分12分)
电信局为了配合客户不同需要,设有A、B两种方案,这两种方案应付话费y(元)与通话时间x(分钟)之间的关系如图(实线部分)所示(注:图中MN∥CD)
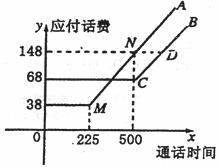
(Ⅰ)求这两种方案的应付话费y与通话时间x的函数关系式fA(x)和fB(x);若通话时间为250分钟,按方案A,B各付话费多少/
(Ⅱ)方案B从500分钟以后,每分钟收费多少元?
(Ⅲ)通话时间在什么范围内方案B才会比方案A优惠?
19.(本小题满分12分)
已知函数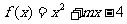 在区间[2,4]上的两全端点处取得最大值和最小值。
在区间[2,4]上的两全端点处取得最大值和最小值。
(Ⅰ)求m的取值范围;
(Ⅱ)试写出函数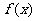 在[2,4]上的最大值g关于m的函数关系式g(m);
在[2,4]上的最大值g关于m的函数关系式g(m);
(Ⅲ)g(m)是否存在最小值?若有,请求出来;若无,请说明理由。
18.(本小题满分10分)
某班一次期末考试之后,从全班同学中随机抽出5位,这5位同学的数学、物理分数见表:
|
学生编号 |
1 |
2 |
3 |
4 |
5 |
|
数学分数x |
70 |
75 |
80 |
85 |
90 |
|
物理分数y |
73 |
77 |
80 |
88 |
86 |
(Ⅰ)研究变量y与x的相关关系时,计算得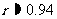 ,这说明y与x的相关程度是怎样的?
,这说明y与x的相关程度是怎样的?
(Ⅱ)求得y与x的线性回归方程之后,若该方程所表示的直线一定过点A,求点A坐标。
(Ⅲ)求得回归方程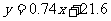 后,请估计该班本次考试数学成绩为60分的学生的物理成绩。
后,请估计该班本次考试数学成绩为60分的学生的物理成绩。
17.(本小题满分10分)
已知对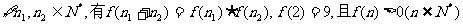 联(Ⅰ)求
联(Ⅰ)求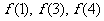 的值
的值
(Ⅱ)试猜想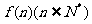 的解析式。
的解析式。
16.一个池有2个进水口,1个出水口,进出水速度如图甲、乙所示。某天0点到6点,该水池的蓄水量如图丙所示。(至少打开一个水口)
给出以下3个论断:①0点到3点只进水不出水;②3点到4点不进水只出水;
③4点到6点不进水不出水。则一定能够确定正确的论断序号是 .
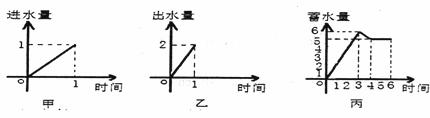
15.任意实x,符号[x]表示“不超过x的最大整数”,如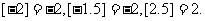 则
则 = .
= .
14.已知偶函数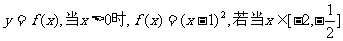 时,不等式
时,不等式
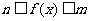 恒成立,则m-n的最小值是 .
恒成立,则m-n的最小值是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com